题目内容
 如图,顶点为A的抛物线y=a(x+2)2-4交x轴于点B(1,0),连接AB,过原点O作射线OM∥AB,过点A作AD∥x轴交OM于点D,点C为抛物线与x轴的另一个交点,连接CD.
如图,顶点为A的抛物线y=a(x+2)2-4交x轴于点B(1,0),连接AB,过原点O作射线OM∥AB,过点A作AD∥x轴交OM于点D,点C为抛物线与x轴的另一个交点,连接CD.
(1)求抛物线的解析式(关系式);
(2)求点A,B所在的直线的解析式(关系式);
(3)若动点P从点O出发,以每秒1个单位长度的速度沿着射线OM运动,设点P运动的时间为t秒,问:当t为何值时,四边形ABOP分别为平行四边形?等腰梯形?
(4)若动点P从点O出发,以每秒1个单位长度的速度沿线段OD向点D运动,同时动点Q从点C出发,以每秒2个单位长度的速度沿线段CO向点O运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动时间为t秒,连接PQ.问:当t为何值时,四边形CDPQ的面积最小?并求此时PQ的长.
 解:(1)把(1,0)代入y=a(x+2)2-4,
解:(1)把(1,0)代入y=a(x+2)2-4,得a=
 .
.∴y=
 (x+2)2-4,
(x+2)2-4,即y=
 x2+
x2+ x-
x- .
.(2)设直线AB的解析式是y=kx+b.
∵点A(-2,-4),点B(1,0),
∴

解得

∴y=
 x-
x- .
.(3)由题意得OP=t,AB=
 =5.
=5.若四边形ABOP为平行四边形,则OP=AB=5,即当t=5时,四边形ABOP为平行四边形.
若四边形ABOP为等腰梯形,连接AP,过点P作PG⊥AB,过点O作OH⊥AB,垂足分别为G、H.
∴△APG≌△BOH.
在Rt△OBM中,
∵OM=
 ,OB=1,
,OB=1,∴BM=
 .
.∴OH=
 .
.∴BH=
 .
.∴OP=GH=AB-2BH=
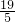 .
.即当t=
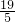 时,四边形ABOP为等腰梯形.
时,四边形ABOP为等腰梯形.(4)将y=0代入y=
 x2+
x2+ x-
x- ,得
,得 x2+
x2+ x-
x- =0,
=0,解得x=1或-5.
∴C(-5,0).
∴OC=5.
∵OM∥AB,AD∥x轴,
∴四边形ABOD是平行四边形.
∴AD=OB=1.
∴点D的坐标是(-3,-4).
∴S△DOC=
 ×5×4=10.
×5×4=10.过点P作PN⊥BC,垂足为N.易证△OPN∽△BOH.
∴
 ,
,即
 .
.∴PN=
 t.
t.∴四边形CDPQ的面积S=S△DOC-S△OPQ=10-
 ×(5-2t)×
×(5-2t)× t=
t= t2-2t+10.
t2-2t+10.∴当t=
 时,四边形CDPQ的面积S最小.
时,四边形CDPQ的面积S最小.此时,点P的坐标是(-
 ,-1),点Q的坐标是(-
,-1),点Q的坐标是(- ,0),
,0),∴PQ=
 =
=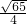 .
.分析:(1)将点B的坐标代入到抛物线的解析式中即可求得a值,从而求得其解析式;
(2)将点A和点B的坐标代入到直线的解析式利用待定系数法确定其解析式即可;
(3)利用两点坐标求得线段AB的长,然后利用平行四边形的对边相等求得t=5时,四边形ABOP为平行四边形;若四边形ABOP为等腰梯形,连接AP,过点P作PG⊥AB,过点O作OH⊥AB,垂足分别为G、H,根据△APG≌△BOH求得线段OP=GH=AB-2BH=
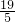 .
.(4)首先判定四边形ABOD是平行四边形,然后确定S△DOC=
 ×5×4=10.过点P作PN⊥BC,垂足为N,利用△OPN∽△BOH得到PN=
×5×4=10.过点P作PN⊥BC,垂足为N,利用△OPN∽△BOH得到PN= t,然后表示出四边形CDPQ的面积S=S△DOC-S△OPQ=10-
t,然后表示出四边形CDPQ的面积S=S△DOC-S△OPQ=10- ×(5-2t )×
×(5-2t )× t=
t= t2-2 t+10,从而得到当t=
t2-2 t+10,从而得到当t= 时,四边形CDPQ的面积S最小.然后得到点P的坐标是(-
时,四边形CDPQ的面积S最小.然后得到点P的坐标是(- ,-1),点Q的坐标是(-
,-1),点Q的坐标是(- ,0),利用两点坐标公式确定PQ的长即可.
,0),利用两点坐标公式确定PQ的长即可.点评:本题考查了二次函数的综合知识,往往是中考的压轴题目,难度比较大.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
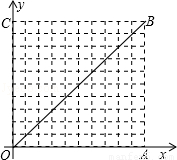
 (2013•湖州)如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为
(2013•湖州)如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为 如图,一个隧道的横截面成抛物线形,它的底部宽12米、高6米.车辆在此隧道可以双向通行,但规定车辆必须在隧道的中心线右侧、距离路边缘2米这一范围内行驶,并保持车辆顶部与隧道的空隙不少于
如图,一个隧道的横截面成抛物线形,它的底部宽12米、高6米.车辆在此隧道可以双向通行,但规定车辆必须在隧道的中心线右侧、距离路边缘2米这一范围内行驶,并保持车辆顶部与隧道的空隙不少于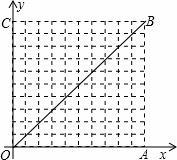
 米.
米.
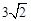 ,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是
,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是