题目内容
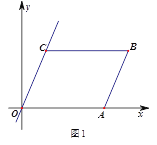
【题目】如图，在平面直角坐标系中，四边形OABC是平行四边形．直线L经过O、C两点．点A的坐标为（8，0），点B的坐标为（11，4），动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动，同时动点Q从点A出发以每秒2个单位的速度沿A→B→C的方向向点C运动，过点P作PM垂直于x轴，与折线O一C﹣B相交于点M．当Q、M两点相遇时，P、Q两点停止运动，设点P、Q运动的时间为t秒（t＞0）．△MPQ的面积为S．
（1）点C的坐标为 ，直线L的解析式为 ．
（2）试求点Q与点M相遇前S与t的函数关系式，并写出相应的t的取值范围．
（3）试求题（2）中当t为何值时，S的值最大，并求出S的最大值．
（4）随着P、Q两点的运动，当点M在线段CB上运动时，设PM的延长线与直线L相交于点N．试探究：当t为何值时，△QMN为等腰三角形？请直接写出t的值．
【答案】（1）（3，4），y= 
x；（2）①当0＜t≤
，S= 
t2+ 
t；②当＜t≤3时，S= －2t2+
t, ③当点Q与点M相遇时，S=﹣6t+32；(3) 当
时，S有最大值，最大值为
.(4) 当t=
时，△QMN为等腰三角形．
【解析】（1）由平行四边形的性质和点A、B的坐标便可求出C点坐标，将C点坐标代入正比例函数即可求得直线l的解析式；
（2）根据题意，得OP=t，AQ=2t，根据t的取值范围不同分三种情况分别进行讨论，得到三种S关于t的函数，解题时注意t的取值范围；
（3）分别根据三种函数解析式求出当t为何值时，S最大，然后比较三个最大值，可知当t=
时，S有最大值，最大值为
；
（4）根据题意并细心观察图象，分两种情况讨论可知：当t=
时，△QMN为等腰三角形．
解：（1）由题意知：点A的坐标为（8，0），点B的坐标为（11.4），
且OA=BC，故C点坐标为C（3，4），设直线l的解析式为y=kx，将C点坐标代入y=kx，解得k=
，
∴直线l的解析式为y= x；故答案为：（3，4），y= x；
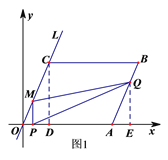
（2）根据题意，得OP=t，AQ=2t．分四种情况讨论：
①当0＜t≤
时，如图1，M点的坐标是（t， t）．过点C作CD⊥x轴于D，过点Q作QE⊥x轴于E，可得△AEQ∽△ODC，∴ 
= 
=
，∴ 
= 
=
，∴AE =
，EQ= 
t，∴Q点的坐标是（8+ 
t， t），∴PE=8+t－t= 8+
t，∴S=
·MP·PE=
·
t·（8+
t）= 
t2+ 
t；
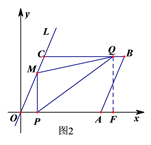
②当＜t≤3时，如图2，过点Q作QF⊥x轴于F，∵BQ=2t﹣5，∴OF=11﹣（2t﹣5）=16﹣2t，
∴Q点的坐标是（16﹣2t，4），∴PF=16﹣2t﹣t=16﹣3t，
∴S=·MP·PF=·t·(16－3t)= －2t2+
t,
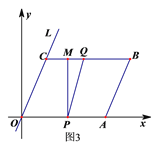
③当点Q与点M相遇时，16﹣2t=t，解得t =
．当3＜t＜时，如图3，MQ=16﹣2t﹣t=16﹣3t，MP=4．S=·MP·PF =·4·（16－3t）=﹣6t+32；
（3）解：① 当
时，
，∵
，抛物线开口向上，对称轴为直线
， ∴ 当时，S随t的增大而增大.
∴ 当
时，S有最大值，最大值为
．
②当
时，
。∵
，抛物线开口向下．
∴当时，S有最大值，最大值为．
③当
时，
，∵
．∴S随t的增大而减小．
又∵当
时，S=14．当
时，S=0．∴
．
综上所述，当时，S有最大值，最大值为.
（4）M、Q在BC边上运动且没有相遇时，如图4，CM=t－3，BQ= 2t－5，MN=（t－3），∴MQ= 8－（t－3）－（2t－5）= 16－3t，∴只有（t－3）=16－3t，即当t=
时，△QMN为等腰三角形．
“点睛”本题是二次函数的综合题，其中涉及到的知识点有抛物线最大值的求法和动点问题等知识点，是各地中考的热点和难点，解题时注意数形结合和分类讨论等数学思想的运用，同学们要加强训练，属于难题．
