题目内容
一元二次方程x2-2x-3=0的根为（ ）A．x1=1，x2=3
B．x1=-1，x2=3
C．x1=-1，x2=-3
D．x1=1，x2=3
【答案】分析：方程左边的多项式利用十字相乘法分解因式后，利用两数相乘积为0，两因式中至少有一个为0转化为两个一元一次方程，求出一次方程的解即可得到原方程的解．
解答：解：x2-2x-3=0，
分解因式得：（x-3）（x+1）=0，
可得x-3=0或x+1=0，
解得：x1=-1，x2=3．
故选B．
点评：此题考查了解一元二次方程-因式分解法，利用此方法解方程时，首先将方程右边化为0，左边化为积的形式，然后利用两数相乘积为0，两因式中至少有一个为0转化为两个一元一次方程来求解．
解答：解：x2-2x-3=0，
分解因式得：（x-3）（x+1）=0，
可得x-3=0或x+1=0，
解得：x1=-1，x2=3．
故选B．
点评：此题考查了解一元二次方程-因式分解法，利用此方法解方程时，首先将方程右边化为0，左边化为积的形式，然后利用两数相乘积为0，两因式中至少有一个为0转化为两个一元一次方程来求解．
练习册系列答案
新思维寒假作业系列答案
相关题目
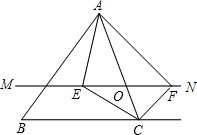从甲、乙两题中选做一题，如果两题都做，只以甲题计分．