题目内容
 同心圆O中,大圆的弦EF切小圆于K,EP切小圆于P,FQ切小圆于Q,G为小圆
同心圆O中,大圆的弦EF切小圆于K,EP切小圆于P,FQ切小圆于Q,G为小圆 上一点,GE、GF分别交小圆于M、N两点,下列四个结论:①EM=MG;②FQ2=FN•NG;③EP=FQ;④FN•FG=EM•EG.正确的结论为
上一点,GE、GF分别交小圆于M、N两点,下列四个结论:①EM=MG;②FQ2=FN•NG;③EP=FQ;④FN•FG=EM•EG.正确的结论为
- A.①③
- B.②③
- C.③④
- D.②④
C
分析:连接OK,根据垂径定理得EK=FK,OK垂直于EF,由切线长定理,EP=EK,FQ=FK,从而得出EP=FQ,再由切割线定理得,
FK2=FN•FG,EK2=EM•EG;则FN•FG=EM•EG,从而得出答案.
解答: 解:连接OK,
解:连接OK,
∵EF切小圆于K,∴OK⊥EF,根据垂径定理得EK=FK,
∵EP切小圆于P,FQ切小圆于Q,
∴EP=EK,FQ=FK,
∴EP=FQ,
故③正确;
∴由切割线定理得,FK2=FN•FG,EK2=EM•EG,
∴FN•FG=EM•EG,
故④正确;
故选C.
点评:本题是基础题,考查了切线的性质、切割线定理以及垂径定理,是中考的热点,要掌握牢固.
分析:连接OK,根据垂径定理得EK=FK,OK垂直于EF,由切线长定理,EP=EK,FQ=FK,从而得出EP=FQ,再由切割线定理得,
FK2=FN•FG,EK2=EM•EG;则FN•FG=EM•EG,从而得出答案.
解答:
 解:连接OK,
解:连接OK,∵EF切小圆于K,∴OK⊥EF,根据垂径定理得EK=FK,
∵EP切小圆于P,FQ切小圆于Q,
∴EP=EK,FQ=FK,
∴EP=FQ,
故③正确;
∴由切割线定理得,FK2=FN•FG,EK2=EM•EG,
∴FN•FG=EM•EG,
故④正确;
故选C.
点评:本题是基础题,考查了切线的性质、切割线定理以及垂径定理,是中考的热点,要掌握牢固.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
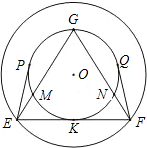 同心圆O中,大圆的弦EF切小圆于K,EP切小圆于P,FQ切小圆于Q,G为小圆
同心圆O中,大圆的弦EF切小圆于K,EP切小圆于P,FQ切小圆于Q,G为小圆

 2DE.
2DE.

 上一点,GE、GF分别交小圆于M、N两点,下列四个结论:①EM=MG;②FQ2=FN•NG;③EP=FQ;④FN•FG=EM•EG.正确的结论为( )
上一点,GE、GF分别交小圆于M、N两点,下列四个结论:①EM=MG;②FQ2=FN•NG;③EP=FQ;④FN•FG=EM•EG.正确的结论为( )