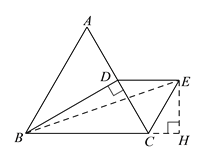
题目内容
【题目】如图,△ABC为等边三角形,过点B作BD⊥AC于点D,过D作DE∥BC,且DE=CD,连接CE,
(1)求证:△CDE为等边三角形;
(2)请连接BE,若AB=4,求BE的长.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)由△ABC为等边三角形得∠ACB=60°,又DE∥BC知∠EDC=60°,且DE=DC,从而可证△CDE为等边三角形;
(2)过点E作EH⊥BC于H,求出EH和CH的长,利用勾股定理即可求出BE的长.
试题解析:(1)∵△ABC为等边三角形
∴∠ACB=60°
∵DE∥BC
∴∠EDC=∠ACB=60°
又∵DE=DC
∴△CDE为等边三角形
(2)过点E作EH⊥BC于H
∵BD⊥AC ∴CD=![]() AC=
AC=![]() AB=2
AB=2
又∵△CDE为等边三角形
∴CE=CD=2
∵∠ECH=60°
∴EH=EC·sin60°=2×![]() =
=![]() ,CH=EC·cos60°=1
,CH=EC·cos60°=1
∴![]()

练习册系列答案
相关题目
【题目】学校准备设计一款女生校服,对全校女生喜欢的颜色进行了问卷调查,统计如下表所示:
颜色 | 黄色 | 绿色 | 白色 | 紫色 | 红色 |
学生人数 | 100 | 180 | 220 | 80 | 750 |
学校决定采用红色,可用来解释这一现象的统计知识是( )
A. 平均 B. 中位数 C. 众数 D. 方差
