题目内容
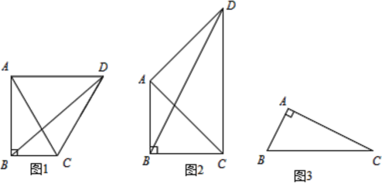
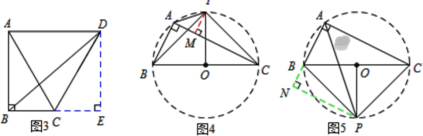
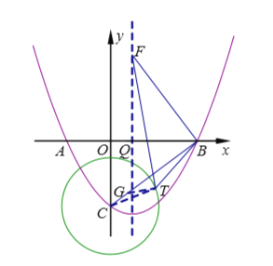
【题目】如图，抛物线y=ax2－2ax+c与x轴分别交于点A、B(点B在点A的右侧)，与y轴交于点C，连接BC，点(
，
a－3)在抛物线上．
（1）求c的值；
（2）已知点D与C关于原点O对称，作射线BD交抛物线于点E，若BD=DE，①求抛物线所对应的函数表达式 ；②过点B作BF⊥BC交抛物线的对称轴于点F，以点C为圆心，以
的长为半径作⊙C，点T为⊙C上的一个动点，求
TB+TF的最小值．
【答案】（1）
；（2）①抛物线的解析式为
；②
【解析】
（1）将
代入
中即可求得c的值；
（2）①根据题意，设点
，则点
，将两点坐标代入
中即可求得a的值，进而即可求得函数解析式；
②根据题意，令y=0求出
，再由
及勾股定理求得
，接着由
得到
，再根据当点F，T，G三点共线时，
的值最小，最小值为线段
的长进而即可求得最小值．
解：（1）∵点在抛物线上
；
（2）①如图，由题意，得点
点
与点
关于原点
对称
点
设点，则点
将，代入抛物线
得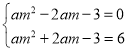
解得
抛物线的解析式为；
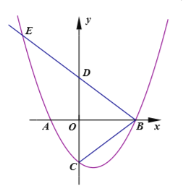
②∵抛物线
抛物线的对称轴为直线
令
，则
解得
或
如图，设直线与
轴的交点为
，则
，
又
在
中，
，，由勾股定理得
在
上截取，
，取
，
又
，即
点
为定点
当点F，T，G三点共线时，的值最小，最小值为线段的长
在
中，
，
，由勾股定理得：
．
练习册系列答案
相关题目
