��Ŀ����
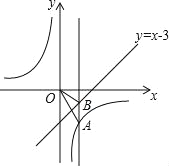
����Ŀ����ƽ��ֱ������ϵ�У�������![]() �Ķ���
�Ķ���![]() ��ֱ��
��ֱ��![]() �ϣ�
�ϣ�
��1����ֱ�ߵĺ�������ʽ��
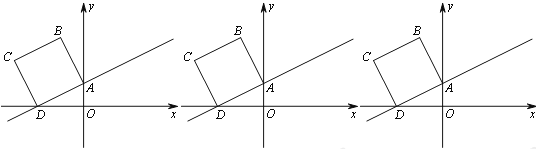
��2���ֽ��������ظ�ֱ�߷������ƽ�ƣ�ƽ�ƺ�������ߵĶ���Ϊ��![]() ����ֱ�ߵ���һ������Ϊ��
����ֱ�ߵ���һ������Ϊ��![]() ����
����![]() ����ҽ���Ϊ��
����ҽ���Ϊ��![]() ����
����![]() �����
�����![]() �غϣ�������
�غϣ�������![]() ��
��![]() ��
��
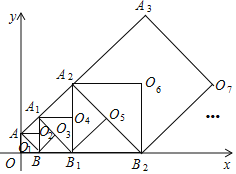
����ͼ����ƽ�ƹ����У�����![]() �ڵ���������
�ڵ���������![]() �����Ϊ60ʱ����ƽ�Ƶľ���
�����Ϊ60ʱ����ƽ�Ƶľ���![]() �ij���
�ij���
����ƽ�ƹ����У���![]() �����߶�
�����߶�![]() Ϊһ��ֱ�DZߵ�ֱ��������ʱ������������������ĵ�
Ϊһ��ֱ�DZߵ�ֱ��������ʱ������������������ĵ�![]() �����꣮
�����꣮
���𰸡���1��![]() ����2����
����2����![]() ����
����![]() ��
��![]() ��
��
��������
��1�������䷽���������߱���ʽ����Ϊ����ʽ���ɴ˿ɵó���A�����꣬���ݵ�A�����꣬���ô���ϵ�����������ֱ�ߵĺ�������ʽ��
��2�����A��������Ϊ��m����2m��2������ƽ�ƺ������ߵĺ�������ʽΪy��![]() ��x��m��2��2m��2������һ�κ���ͼ���ϵ������������ϵ�C��x�����ҵ�C�����A���غϣ��ɵó�m����1��
��x��m��2��2m��2������һ�κ���ͼ���ϵ������������ϵ�C��x�����ҵ�C�����A���غϣ��ɵó�m����1��
������ֱ�ߺ������ߵı���ʽ�ɷ����飬ͨ���ⷽ����������B�������꣬���ö��κ���ͼ���ϵ�����������������C�����꣬����C��CD��y�ᣬ��ֱ��A��B���ڵ�D���ɵ�C������ɵó���D�����꣬����S��A��B��C��S��B��CD��S��A��CD��60�����ɵó�����t�ķ��̣����û�Ԫ���ⷽ���鼴�ɵó�m��ֵ�������ɵó���A�������꣬���ɵ�A���������������ľ��빫ʽ����������ۣ�
�ڸ��ݵ�A����B����C�����꣬�ɵó�A��B����A��C��B��C�ij��ȣ��֡�A��B��C��90������B��A��C��90��������������ù��ɶ����ɵó�����m�ķ��̣����û�Ԫ���ⷽ�̼������m��ֵ�������ɵó���A�������꣬����ý⣮
��1����y��![]() ��6x+4��
��6x+4��![]() ��x��6��2��14��
��x��6��2��14��
���A��������6����14����
�ߵ�A��ֱ��y��kx��2�ϣ�
�ੁ14��6k��2����ã�k����2��
��ֱ�ߵĺ�������ʽΪy����2x��2��
��2�����A��������Ϊ��m����2m��2������ƽ�ƺ������ߵĺ�������ʽΪy��![]() ��x��m��2��2m��2��
��x��m��2��2m��2��
��y��0ʱ���Щ�2x��2��0��
��ã�x����1��
��ƽ�ƺ����������x����ҽ���ΪC����C�����A���غϣ���
��m����1��
������ֱ���������ߵı���ʽ�ɷ����飬 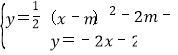
��ã�![]() ��
��![]() ��
��
���B����������m��4����2m+6����
��y��0ʱ����![]() ��x��m��2��2m��2��0��
��x��m��2��2m��2��0��
��ã�x1��m��2![]() ��x2��m+2
��x2��m+2![]() ��
��
���C��������m+2![]() ��0����
��0����
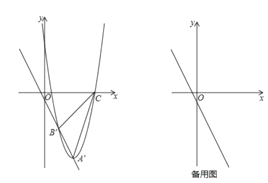
����C��CD��y�ᣬ��ֱ��A��B���ڵ�D����ͼ��ʾ��
��x��m+2![]() ʱ��y����2x��2����2m��4
ʱ��y����2x��2����2m��4![]() ��2��
��2��
���D��������m+2![]() ����2m��4
����2m��4![]() ��2����
��2����
��CD��2m+2+4![]() ��
��
��S��A��B��C��S��B��CD��S��A��CD��![]() CD[m+2
CD[m+2![]() ����m��4��]��
����m��4��]��![]() CD��m+2
CD��m+2![]() ��m����2CD��2��2m+2+4
��m����2CD��2��2m+2+4![]() ����60��
����60��
��t��![]() ������t2+2t��15��0��
������t2+2t��15��0��
��ã�t1����5����ȥ����t2��3��
��m��8��
���A����������8����18����
��AA����![]() ��
��
�ڡ�A����m����2m��2����B����m��4����2m+6����C��m+2![]() ��0����
��0����
��A��B��2����m��4��m��2+[��2m+6������2m��2��]2��80��A��C2����m+2![]() ��m��2+[0������2m��2��]2��4m2+12m+8��B��C2��[m+2
��m��2+[0������2m��2��]2��4m2+12m+8��B��C2��[m+2![]() ����m��4��]2+[0������2m+6��]2��4m2��20m+56+16
����m��4��]2+[0������2m+6��]2��4m2��20m+56+16![]() ��
��
����A��B��C��90��ʱ����A��C2��A��B��2+B��C2����4m2+12m+8��80+4m2��20m+56+16![]() ��
��
�����ã�32m��128��16![]() ��0��
��0��
��a��![]() ������2a2��a��10��0��
������2a2��a��10��0��
��ã�a1����2����ȥ����a2��![]() ��
��
��m��![]() ��
��
���A��������Ϊ![]() ��
��
����B��A��C��90��ʱ����B��C2��A��B��2+A��C2����4m2��20m+56+16![]() ��80+4m2+12m+8��
��80+4m2+12m+8��
�����ã�32m+32��16![]() ��0��
��0��
��a��![]() ������2a2��a��0��
������2a2��a��0��
��ã�a3��0����ȥ����a4��![]() ��
��
��m����![]() ��
��
���A��������Ϊ![]() ��
��
������������ƽ�ƹ����У�����A��B��C����A��B��Ϊһ��ֱ�DZߵ�ֱ��������ʱ����A��������Ϊ![]() ��
��![]() ��
��

 ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д�