Question

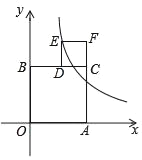
【题目】在平面直角坐标系xOy中，直线l：y＝ax+b与双曲线交于点A（1，m）和B（﹣2，﹣1）．点A关于x轴的对称点为点C．

（1）①求k的值和点C的坐标；②求直线l的表达式；

（2）过点B作y轴的垂线与直线AC交于点D，经过点C的直线与直线BD交于点E．若30°≤∠CED≤45°，直接写出点E的横坐标t的取值范围．

Answer 1

【答案】（1）①k=2；点C为（1,-2）.

②直线l的表达式为.

（2） 或.

【解析】

（1）①将B点坐标带入，得到k值，再将A点带入双曲线，得到m值，由对称性得到点C.

②由①可知A，B两点坐标，将它们带入y=ax＋b，列方程组得到直线l的表达式.

（2）结合题意根据三角函数关系即可得到答案.

（1）①将B点坐标带入，

则，

得到k=2，则双曲线为，

再将A点带入双曲线，

则

得到m=2值，则点A为（1，2），由对称性得到点C为（1,-2）.

②由①可知A，B两点坐标，将它们带入y=ax＋b，

列方程组

两式相加得b=0,则a=.故直线l的表达式为.

（2）由题意可知C到BD的距离为1，因为，

当时，DE1=DE4=1,∴t=0或t=2;当时，DE2=DE3=

可得t= 或t=，∴ 或.