Question

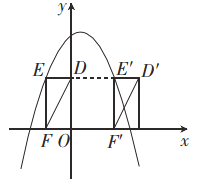
【题目】如图，四边形ABCO为矩形，点A在x轴上，点C在y轴上，且点B的坐标为（2,1），将此矩形绕点O逆时针旋转90°得矩形DEFO，抛物线y=-x2+bx+c过B、E两点.

（1）求此抛物线的函数解析式.

（2）将矩形DEFO向右平移，当点E的对应点E’在抛物线上时，求线段DF扫过的面积.

（3）若将矩形ABCO向上平移d个单位长度后，能使此抛物线的顶点在此矩形的边上，求d的值.

Answer 1

【答案】（1）；（2）平行四边形DD’F’F的面积为；（3） 平移的距离或.

【解析】

（1）直接利用待定系数法即可解决问题．

（2）由平移可知DF扫过的面积为平行四边形DD’F’F的面积.根据点E向右平移后的对应点E’在抛物线上，可得E’的坐标，从而求出平移的距离即可求出面积。

（3）求出抛物线顶点坐标，点B坐标，即可解决问题．

⑴由题意可知，点E的坐标为（-1,2）.

把（2,1），（-1,2）分别代入，

可得，解得.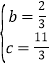

∴此抛物线的解析式为.

⑵如图，由平移可知DF扫过的面积为平行四边形DD’F’F的面积.

当点E向右平移后的对应点E’在抛物线上时，

有，则，解得，，

∴E’（），

∴，

∴平行四边形DD’F’F的面积为.

⑶∵，

∴抛物线的顶点坐标为（），

∵B（2,1），

∴平移的距离或.