题目内容
设x1,x2是方程x2-(k+1)x-3=0的两根,且 ,求k的值.
,求k的值.
解:∵x1,x2是方程x2-(k+1)x-3=0的两根,
∴x1+x2=k+1,x1x2=-3,
∵ +
+ =
=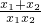 =
= =2,
=2,
解得:k=-7.
分析:利用根与系数的关系表示出两根之和与两根之积,将已知等式左边通分并利用同分母分式的加法法则变形,把各自的值代入即可求出k的值.
点评:此题考查了根与系数的关系,熟练掌握根与系数的关系是解本题的关键.
∴x1+x2=k+1,x1x2=-3,
∵
 +
+ =
=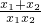 =
= =2,
=2,解得:k=-7.
分析:利用根与系数的关系表示出两根之和与两根之积,将已知等式左边通分并利用同分母分式的加法法则变形,把各自的值代入即可求出k的值.
点评:此题考查了根与系数的关系,熟练掌握根与系数的关系是解本题的关键.

练习册系列答案
相关题目
设x1、x2是方程2x2-6x+3=0的两个根,那么x12+x22的值为( )
| A、3 | B、-3 | C、6 | D、-6 |
设x1、x2是方程
x2-x-3=0的两个根,则有( )
| 1 |
| 3 |
| A、x1+x2=-1 |
| B、x1x2=-9 |
| C、x1x2=1 |
| D、x1x2=9 |
设x1、x2是方程3x2-7x-6=0的两根,则(x1-3)•(x2-3)=( )
| A、6 | B、4 | C、2 | D、0 |