题目内容
解方程组 .
.
解:由①得x-y=1或x-y=-1,即x=y+1或x=y-1.与②结合有下面两个方程组,
(1)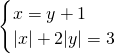 ,
,
把x=y+1代入|x|+2|y|=3得,|y+1|+2|y|=3.
去绝对值符号,可得y= 或y=-
或y=- ,再将其代入x=y+1可求出方程组(1)的解为:
,再将其代入x=y+1可求出方程组(1)的解为:
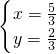 或
或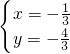 ,
,
(2)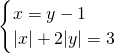 ,
,
把x=y-1代入|x|+2|y|=3得,|y-1|+2|y|=3.
去绝对值符号,可得y=- 或y=-
或y=- ,再将其代入x=y-1可求出方程组(1)的解为:
,再将其代入x=y-1可求出方程组(1)的解为:
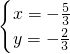 或
或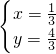 .
.
故原方程组的解为:
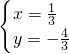 ,
,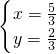 ,
,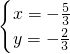 或
或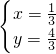 .
.
分析:先根据绝对值的性质把①中的绝对值符号去掉,把由①得到的方程与②联立得到关于x、y的两个方程组,再分别求出两组方程组的解即可.
点评:本题考查的是解二元一次方程组及绝对值的性质,能根据题意得到关于x、y的两组方程组是解答此题的关键.
(1)
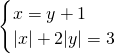 ,
,把x=y+1代入|x|+2|y|=3得,|y+1|+2|y|=3.
去绝对值符号,可得y=
 或y=-
或y=- ,再将其代入x=y+1可求出方程组(1)的解为:
,再将其代入x=y+1可求出方程组(1)的解为: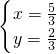 或
或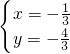 ,
,(2)
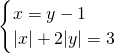 ,
,把x=y-1代入|x|+2|y|=3得,|y-1|+2|y|=3.
去绝对值符号,可得y=-
 或y=-
或y=- ,再将其代入x=y-1可求出方程组(1)的解为:
,再将其代入x=y-1可求出方程组(1)的解为: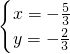 或
或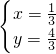 .
.故原方程组的解为:
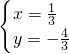 ,
,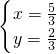 ,
,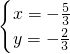 或
或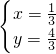 .
.分析:先根据绝对值的性质把①中的绝对值符号去掉,把由①得到的方程与②联立得到关于x、y的两个方程组,再分别求出两组方程组的解即可.
点评:本题考查的是解二元一次方程组及绝对值的性质,能根据题意得到关于x、y的两组方程组是解答此题的关键.

练习册系列答案
相关题目
 (1)解方程组:
(1)解方程组: