Question

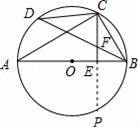
如图，AB是⊙O的直径，C是的中点，CE⊥AB于E，BD交CE于点F．

（1）求证：CF=BF；

（2）若CD=6，AC=8，求⊙O的半径．

Answer 1

【考点】圆周角定理；勾股定理；圆心角、弧、弦的关系．

【分析】（1）首先延长CE交⊙O于点P，由垂径定理可证得∠BCP=∠BDC，又由C是的中点，易证得∠BDC=∠CBD，继而可证得CF=BF；

（2）由AB是⊙O的直径，根据直径所对的圆周角是直角，可得∠ACB=90°，然后由勾股定理求得AB的长，继而求得答案．

【解答】（1）证明：延长CE交⊙O于点P，

∵CE⊥AB，

∴=，

∴∠BCP=∠BDC，

∵C是的中点，

∴CD=CB，

∴∠BDC=∠CBD，

∴∠CBD=∠BCP，

∴CF=BF；

（2）解：∵AB是⊙O的直径，

∴∠ACB=90°，

∵CD=6，AC=8，

∴BC=6，

在Rt△ABC中，AB=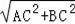=10，

∴⊙O的半径为5．