题目内容
如图，已知等腰△ABC的底边BC=13cm，D是腰AB上一点，且CD=12cm，BD=5cm．（1）求证：△BDC是直角三角形；
（2）求△ABC的周长．
分析：（1）由BC=13cm，CD=12cm，BD=5cm，知道BC2=BD2+CD2，所以△BDC为直角三角形，
（2）由（1）可求出AC的长，周长即可求出．
（2）由（1）可求出AC的长，周长即可求出．
解答：（1）证明：∵BC=13cm，CD=12cm，BD=5cm，
∴BC2=BD2+CD2
∴△BDC为直角三角形；
（2）解：设AB=x，
∵△ABC是等腰三角形，
∴AB=AC=x，
∵AC2=AD2+CD2
x2=（x-5）2+122，
解得：x=
，
∴△ABC的周长=2AB+BC=26+
=
．
∴BC2=BD2+CD2
∴△BDC为直角三角形；
（2）解：设AB=x，
∵△ABC是等腰三角形，
∴AB=AC=x，
∵AC2=AD2+CD2
x2=（x-5）2+122，
解得：x=
| 169 |
| 10 |
∴△ABC的周长=2AB+BC=26+
| 169 |
| 10 |
| 429 |
| 10 |
点评：此题考查等腰三角形的性质、勾股定理以及逆定理的应用，属于基础题目．
练习册系列答案
相关题目
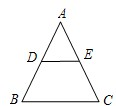如图，已知等腰△ABC的面积为8cm2，点D，E分别是AB，AC边的中点，则梯形DBCE的面积为
如图，已知等腰三角形ADC，AD=AC，B是线段DC上的一点，连接AB，且有AB=DB．
（2010•西藏）如图，已知等腰△ABC，AC=BC=10，AB=12，以BC为直径作⊙O交AB点D，交AC于点G，DF⊥AC，垂足为F，交CB的延长线于点E．
如图，已知等腰△ABC中，AB=AC，P、Q分别为AC、AB上的点，且AP=PQ=QB=BC，则∠PCQ的度数为（ ）
如图，已知等腰Rt△ABC中，∠ACB=90°，AC=BC=4，D为△ABC的一个外角∠ABF的平分线上一点，且∠ADC=45°，CD交AB于E，