Question

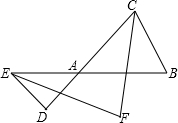如图，点E和D分别在△ABC的边BA和CA的延长线上，CF、EF分别平分∠ACB和∠AED，若∠B=70°，∠D=60°，则∠F的大小是

65°

．

Answer 1

分析：由CF、EF分别平分∠ACB和∠AED，得∠3=∠4，∠1=∠2，所以有∠3+∠B=∠2+∠F；∠3+∠4+∠B=∠1+∠2+∠D，即2∠3+∠B=2∠2+∠D，而∠B=70°，∠D=60°，于是由两个等式即可求出∠F．

解答：解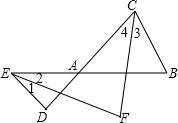：如图，
∵CF、EF分别平分∠ACB和∠AED，
∴∠3=∠4，∠1=∠2，
而∠3+∠B=∠2+∠F；
∠3+∠4+∠B=∠1+∠2+∠D，即2∠3+∠B=2∠2+∠D，
又∵∠B=70°，∠D=60°，
∴∠3+70°=∠2+∠F①，
2∠3+70°=2∠2+60°②，
①×2-②得，70°=2∠F-60°，
解得∠F=65°．
故答案为65°．

点评：本题考查了三角形的内角和定理：三角形的内角和为180°．同时考查了角平分线的性质．