题目内容
如图，点
为直线
上的两点，过两点分别作y轴的平行线交双曲线
（
）于
两点. 若
，则
的值为 .
为直线上的两点，过两点分别作y轴的平行线交双曲线（）于两点. 若，则 的值为 .6
根据A，B两点在直线y=x上，分别设A，B两点的坐标为（a，a），（b，b），得到点C的坐标为（a，
），点D的坐标为（b，
），线段AC=a-，线段BD=b-，根据BD=2AC，有b-=2（a-），然后利用勾股定理进行计算求出4OC2-OD2的值
解：设A（a，a），B（b，b），则C（a，），D（b，）
AC=a-，BD=b-
∵BD=2AC，
∴b-=2（a-）
4OC2-OD2=4（a2+
4[(a-)2+2]-[(b-)2+2]
=4(a-)2+8-4(a-)2-2
=6
故答案为：6．
），点D的坐标为（b，），线段AC=a-，线段BD=b-，根据BD=2AC，有b-=2（a-），然后利用勾股定理进行计算求出4OC2-OD2的值解：设A（a，a），B（b，b），则C（a，
），D（b，）AC=a-
，BD=b-∵BD=2AC，
∴b-
=2（a-）4OC2-OD2=4（a2+
4[(a-)2+2]-[(b-)2+2]=4(a-
)2+8-4(a-)2-2=6
故答案为：6．
练习册系列答案
相关题目
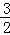x+3
x+3
的图象与反比例函数
的图
，
两点，且点
．求：
的面积．
，
）
，－
经过点
和
轴正半轴上的一点，如果
（为坐标原点）的面积为2，则
的值为 ．
的图象大致是( ).