题目内容
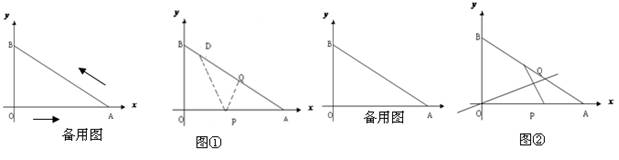
已知:如图,在直角梯形ABCD中,AD∥BC,∠B=90°,CD=8,BC=12,∠ACB=30°,E为BC边上一点,以BE为边作正三角形BEF,使正三角形BEF和梯形ABCD在BC的同侧.
(l)当正三角形BEF的顶点F恰好落在对角线AC上时,求BE的长;
(2)将(1)问中的正三角形BEF沿BC向右平移,记平移中的正三角形BEF为正三角形B′E′F′,当点E与点C重合时停止平移.设平移的距离为x,正三角形B′E′F′的边B′E′和E′F′分别与AC交于点M和点N,连接,DM,DN:
①设正三角形B′E′F′与△ABC重叠部分的面积为S,求S与x之间的函数关系式,并写出自变量x的取值范围,求当DN取得最小值时,求出S的值;
②是否存在这样的x,使三角形DMN是直角三角形?若存在,求出x的值;若不存在,请说明理由.

(l)当正三角形BEF的顶点F恰好落在对角线AC上时,求BE的长;
(2)将(1)问中的正三角形BEF沿BC向右平移,记平移中的正三角形BEF为正三角形B′E′F′,当点E与点C重合时停止平移.设平移的距离为x,正三角形B′E′F′的边B′E′和E′F′分别与AC交于点M和点N,连接,DM,DN:
①设正三角形B′E′F′与△ABC重叠部分的面积为S,求S与x之间的函数关系式,并写出自变量x的取值范围,求当DN取得最小值时,求出S的值;
②是否存在这样的x,使三角形DMN是直角三角形?若存在,求出x的值;若不存在,请说明理由.

分析:(1)如图1,作FQ⊥BC于Q,DH⊥BC于H,根据等边三角形的性质和直角三角形的性质就可以求出BF的值,从而求出BE的值而得出结论;
(2))①如图2,作NG⊥BC于G,根据直角三角形的性质可以求出B′M、MC、E′N的值,再利用三角形的面积公式就可以求出S与x之间的函数关系式,当DN⊥AC时,DN的值最小,在直角三角形中根据勾股定理就可以求出x的值,从而求出此时x的值;
(3)根据图3、图4三种情况当∠DMN=90°、∠DNM=90°或∠MDN=90°时由直角三角形的性质讨论讨论就可以求出x的值,从而得出结论.
(2))①如图2,作NG⊥BC于G,根据直角三角形的性质可以求出B′M、MC、E′N的值,再利用三角形的面积公式就可以求出S与x之间的函数关系式,当DN⊥AC时,DN的值最小,在直角三角形中根据勾股定理就可以求出x的值,从而求出此时x的值;
(3)根据图3、图4三种情况当∠DMN=90°、∠DNM=90°或∠MDN=90°时由直角三角形的性质讨论讨论就可以求出x的值,从而得出结论.
解答:解:(1)如图1,作FQ⊥BC于Q,DH⊥BC于H,
∴∠FQC=∠DHC=90°.
∵AD∥BC,
∴∠DAC=∠6=30°.
∵∠ABC=90°,∠ACB=30°,
∴∠3=60°.
∵BC=12,
∴AB=4
,AC=8
,
∴DH=4
.
∵CD=8,
∴cos∠7=
,
∴∠7=30°,
∴∠DCH=60°,
∴∠8=30°,
∴∠8=∠DAC,
∴AD=DC=8.
∵△BEF是等边三角形,
∴∠1=∠4=60°,BF=BE=EF,
∴∠2=∠5=30°,
∴∠AFB=90°.
∴∠5=∠6,
∴EF=EC.
在Rt△ABF中,由勾股定理,得
AF=2
,BF=6,
∴BE=6.
(2)①如图2,作NG⊥BC于G,
∴∠NGC=90°.
∵∠F′B′C=60°,∠ACB=30°,
∴∠B′MC=90°.
∵BB′=x,
∴B′C=12-x,CE′=12-6-x=6-x
∴B′M=6-
x,MC=6
-
x,E′N=6-x,
∴GE′=3-
x,GN=3
-
x,
∴S=
-
,
S=-
x2+9
,(0≤x≤6),
∵DN最小,
∴DN⊥AC,
在Rt△DNC中,由勾股定理,得
DN=4,CN=4
,
在Rt△GNC中,由勾股定理,得
GN=2
,
在Rt△GNE′中,由勾股定理,得
GE′=2,E′N=4.
∴CE′=4.
∴BB′=12-4-6=2.
∴S=-
×4+9
,
=9
-
=
 ②如图3,当DN⊥AC于N时,作NG⊥BC于G,
②如图3,当DN⊥AC于N时,作NG⊥BC于G,
∴∠DNM=∠DNC=∠NGC=90°,
在Rt△DNC中,由勾股定理,得
DN=4,CN=4
,
在Rt△NGC中,由勾股定理,得
NG=2
,
在RtNGE′中,由勾股定理,得
GE′=2,NE′=4,
∴CE′=4,
∴x=12-6-4=2;
如图4,当DM⊥AC于M时,
∴∠AMC=90°,
在Rt△DMC中由勾股定理,得
DM=3,MC=4
.
∵∠F′B′E′=60°,∠ACB=30°,
∴∠B′MC=90°,
在Rt△B′MC中,由勾股定理,得
B′M=4,B′C=8,
∴x=12-8=4;
通过作图为,当∠MDN=90°时,直角三角形DMN不存在.
故x的值为:2或4.
∴∠FQC=∠DHC=90°.
∵AD∥BC,
∴∠DAC=∠6=30°.
∵∠ABC=90°,∠ACB=30°,
∴∠3=60°.
∵BC=12,
∴AB=4
| 3 |
| 3 |
∴DH=4
| 3 |
∵CD=8,
∴cos∠7=
| ||
| 2 |
∴∠7=30°,
∴∠DCH=60°,
∴∠8=30°,
∴∠8=∠DAC,

∴AD=DC=8.
∵△BEF是等边三角形,
∴∠1=∠4=60°,BF=BE=EF,
∴∠2=∠5=30°,
∴∠AFB=90°.
∴∠5=∠6,
∴EF=EC.
在Rt△ABF中,由勾股定理,得
AF=2
| 3 |
∴BE=6.
(2)①如图2,作NG⊥BC于G,
∴∠NGC=90°.
∵∠F′B′C=60°,∠ACB=30°,
∴∠B′MC=90°.
∵BB′=x,
∴B′C=12-x,CE′=12-6-x=6-x
∴B′M=6-
| 1 |
| 2 |
| 3 |
| ||
| 2 |
∴GE′=3-
| 1 |
| 2 |
| 3 |
| ||
| 2 |

∴S=
(6-
| ||||||||
| 2 |
(6-x)(3
| ||||||
| 2 |
S=-
| ||
| 8 |
| 3 |
∵DN最小,
∴DN⊥AC,
在Rt△DNC中,由勾股定理,得
DN=4,CN=4
| 3 |
在Rt△GNC中,由勾股定理,得
GN=2
| 3 |
在Rt△GNE′中,由勾股定理,得
GE′=2,E′N=4.
∴CE′=4.
∴BB′=12-4-6=2.
∴S=-
| ||
| 8 |
| 3 |
=9
| 3 |
| ||
| 2 |
=
| 17 |
| 2 |
| 3 |
 ②如图3,当DN⊥AC于N时,作NG⊥BC于G,
②如图3,当DN⊥AC于N时,作NG⊥BC于G,∴∠DNM=∠DNC=∠NGC=90°,
在Rt△DNC中,由勾股定理,得
DN=4,CN=4
| 3 |
在Rt△NGC中,由勾股定理,得
NG=2
| 3 |
在RtNGE′中,由勾股定理,得
GE′=2,NE′=4,
∴CE′=4,
∴x=12-6-4=2;
如图4,当DM⊥AC于M时,
∴∠AMC=90°,
在Rt△DMC中由勾股定理,得
DM=3,MC=4
| 3 |
∵∠F′B′E′=60°,∠ACB=30°,
∴∠B′MC=90°,
在Rt△B′MC中,由勾股定理,得
B′M=4,B′C=8,
∴x=12-8=4;
通过作图为,当∠MDN=90°时,直角三角形DMN不存在.
故x的值为:2或4.
点评:本题考查了平行线的性质,等边三角形的性质,直角三角形的性质及图形运动的综合运用,解答时抓住等边三角形的性质和直角三角形的性质是重点.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目