题目内容
四边形ABCD中,BC=8,CD=1,∠ABC=30°,∠BCD=60°,如果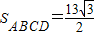 ,则AB的值为( )
,则AB的值为( )A.
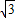
B.
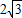
C.
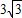
D.
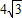
【答案】分析:根据题意画出图形,再分别延长BA与CD相交于E,由三角形内角和定理可得出△BCE是直角三角形,利用勾股定理可求出BE的长,再根据S△BCE=S四边形ABCD+S△ADE求出AB的长即可.
解答: 解:分别延长BA与CD相交于E,则∠BEC=90°,
解:分别延长BA与CD相交于E,则∠BEC=90°,
∴CE= BC=4,
BC=4,
设AB=x,
∵BE= =4
=4  ,
,
∴AE=4 -x,
-x,
∵S△BCE=S四边形ABCD+S△ADE,
即 ×4×4
×4×4  =
= +
+ ×3×(4
×3×(4  -x),
-x),
∴x=4 .
.
故选D.
点评:本题主要考查的是含30度角的直角三角形的知识点,熟练掌握三角形的面积及等积变换,根据题意画出图形,利用数形结合求解是解答此题的关键.
解答:
 解:分别延长BA与CD相交于E,则∠BEC=90°,
解:分别延长BA与CD相交于E,则∠BEC=90°,∴CE=
 BC=4,
BC=4,设AB=x,
∵BE=
 =4
=4  ,
,∴AE=4
 -x,
-x,∵S△BCE=S四边形ABCD+S△ADE,
即
 ×4×4
×4×4  =
= +
+ ×3×(4
×3×(4  -x),
-x),∴x=4
 .
.故选D.
点评:本题主要考查的是含30度角的直角三角形的知识点,熟练掌握三角形的面积及等积变换,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目
 23、如图,四边形ABCD中,对角线AC、BD相交于点E.已知:DA=DC,E为AC中点.
23、如图,四边形ABCD中,对角线AC、BD相交于点E.已知:DA=DC,E为AC中点.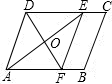 如图所示,在平行四边形ABCD中,AE是∠DAB的平分线,EF∥AD交AB于点F,若AB=9,CE=4,AE=8,则DF等于( )
如图所示,在平行四边形ABCD中,AE是∠DAB的平分线,EF∥AD交AB于点F,若AB=9,CE=4,AE=8,则DF等于( ) 17、如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AB、CD于E、F.请写出图中三对全等的三角形:
17、如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AB、CD于E、F.请写出图中三对全等的三角形: 7、如图,在四边形ABCD中,AD=CB,∠ACB=∠CAD.求证:AB=CD.
7、如图,在四边形ABCD中,AD=CB,∠ACB=∠CAD.求证:AB=CD.