题目内容
已知直线y=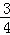 x﹣3与x轴交于点A,与y轴交于点C,抛物线y=﹣
x﹣3与x轴交于点A,与y轴交于点C,抛物线y=﹣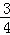 x2+mx+n经过点A和点C.
x2+mx+n经过点A和点C.
(1)求此抛物线的解析式;
(2)在直线CA上方的抛物线上是否存在点D,使得△ACD的面积最大?若存在,求出点D的坐标;若不存在,说明理由.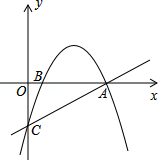
(1)y=﹣ x2+
x2+ x﹣3;(2)存在,D点坐标为(2,
x﹣3;(2)存在,D点坐标为(2, )
)
解析试题分析:(1)由直线的解析式y=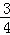 x﹣3,可先求出与坐标轴的交点坐标C点坐标为(0,﹣3),A点坐标为(4,0),然后把A点和C点坐标代入y=﹣
x﹣3,可先求出与坐标轴的交点坐标C点坐标为(0,﹣3),A点坐标为(4,0),然后把A点和C点坐标代入y=﹣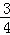 x2+mx+n中得到关于m、n的方程组,解方程组求出m、n即可得到抛物线的解析式;
x2+mx+n中得到关于m、n的方程组,解方程组求出m、n即可得到抛物线的解析式;
(2)过D点作直线AC的平行线y=kx+b,要使△ACD的面积最大,则直线y=kx+b与抛物线只有一个公共点,点D到AC的距离最大,根据两直线平行问题得到k=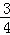 ,过点D的直线解析式为y=
,过点D的直线解析式为y= 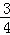 x+b,然后把它与抛物线解析式组成方程组,利用方程组只有一组解和判别式的意义确定b的值,再得到方程组的解,从而得到D点坐标.
x+b,然后把它与抛物线解析式组成方程组,利用方程组只有一组解和判别式的意义确定b的值,再得到方程组的解,从而得到D点坐标.
试题解析:(1)把x=0代入y= x﹣3得y=﹣3,则C点坐标为(0,﹣3),
x﹣3得y=﹣3,则C点坐标为(0,﹣3),
把y=0代入y= x﹣3得
x﹣3得 x﹣3=0,解得x=4,则A点坐标为(4,0),
x﹣3=0,解得x=4,则A点坐标为(4,0),
把A(4,0),C(0,﹣3)代入y=﹣ x2+mx+n得
x2+mx+n得 ,
,
解得 ,
,
所以二次函数解析式为y=﹣ x2+
x2+ x﹣3;
x﹣3;
(2)存在.
过D点作直线AC的平行线y=kx+b,当直线y=kx+b与抛物线只有一个公共点时,点D到AC的距离最大,此时△ACD的面积最大,
∵直线AC的解析式为y= x﹣3,
x﹣3,
∴k= ,即y=
,即y= x+b,
x+b,
由直线y= x+b和抛物线y=﹣
x+b和抛物线y=﹣ x2+
x2+ x﹣3组成方程组得
x﹣3组成方程组得 ,消去y得到3x2﹣12x+4b+12=0,
,消去y得到3x2﹣12x+4b+12=0,
∴△=122﹣4×3×(4b+12)=0,解得b=0,
∴3x2﹣12x+12=0,解得x1=x2=2,
把x=2,b=0代入y= x+b得y=
x+b得y= ,
,
∴D点坐标为(2, ).
).
考点:1.待定系数法求二次函数解析式;2.二次函数图象上点的坐标特征.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,.则a= ,点E的坐标是 .
与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,.则a= ,点E的坐标是 .
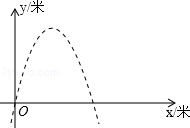
 先向右平移1个单位,再向上平移3个单位,得到新的抛物线解析式是
先向右平移1个单位,再向上平移3个单位,得到新的抛物线解析式是 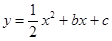 与x轴交于A,B两点,对称轴为直线
与x轴交于A,B两点,对称轴为直线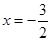 ,直线AD交抛物线于点D(2,3).
,直线AD交抛物线于点D(2,3).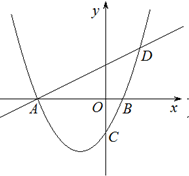
 图象经过A(-1,0),B(4,0)两点.
图象经过A(-1,0),B(4,0)两点.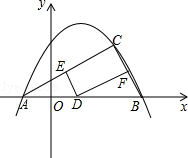
 中,抛物线
中,抛物线 经过点
经过点 (0,
(0, ),
), (3,4).
(3,4). ,点
,点 是抛物线对称轴上一动点,记抛物线在
是抛物线对称轴上一动点,记抛物线在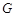 (包含
(包含 与图象
与图象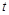 的取值范围.
的取值范围.