��Ŀ����
����Ŀ����ƽ��ֱ������ϵxOy�У���P���Q���غϣ��Ե�PΪԲ��������Q��Բ����Ƹ�ԲΪ��P��Q�ġ����Բ��
��1����֪��P������Ϊ��2��0��������Q������Ϊ��0��1�������P��Q�ġ����Բ���������������Q������Ϊ��3��n�����ҵ�P��Q�ġ����Բ���İ뾶Ϊ![]() ����n��ֵ��
����n��ֵ��
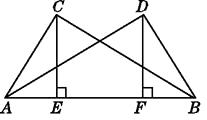
��2����֪��ABCΪ�ȱ������Σ���A�͵�B������ֱ�Ϊ����![]() ��0������
��0������![]() ��0������C��y���������ϣ�����P��Q�ġ����Բ��ǡ���ǡ�ABC������Բ�ҵ�Q��ֱ��y=2x�ϣ����Q�����꣮
��0������C��y���������ϣ�����P��Q�ġ����Բ��ǡ���ǡ�ABC������Բ�ҵ�Q��ֱ��y=2x�ϣ����Q�����꣮
��3����֪��ABC�������������Ϊ��A����3��0����B��![]() ��0����C��0��4������P������Ϊ��0��
��0����C��0��4������P��������0�� ![]() ������Q��������m��
������Q������Ϊ��m�� ![]() ��������P��Q�ġ����Բ�����ABC������������һ�ߴ��ڹ����㣬ֱ��д��m��ȡֵ��Χ��
��������P��Q�ġ����Բ�����ABC������������һ�ߴ��ڹ����㣬ֱ��д��m��ȡֵ��Χ��

���𰸡���1����5�У���2��2����2����![]() ��
�� ![]() ������3��
������3�� ![]() ��
��![]() ��m�ܩ�
��m�ܩ�![]() ��
�� ![]() ��m��
��m��![]() ��
��
�������������������1��������PQ=![]() �������P�İ뾶���ɽ�����⣻
�������P�İ뾶���ɽ�����⣻
������Q��QH��x����H�����ù��ɶ������QH��ֵ�����ɽ�����⣻
��2����Rt��OAC�У���ACO=30�����ɵ�OC=![]() OA=3���Ƴ�C������Ϊ��0��3�����Ƴ���ABC������Բ��Բ�ĵ�����Ϊ��0��1�����뾶Ϊ1���Ƴ�P��0��1������Q��x��2x��������x2+��2x��1��2=1�����x���ɣ�
OA=3���Ƴ�C������Ϊ��0��3�����Ƴ���ABC������Բ��Բ�ĵ�����Ϊ��0��1�����뾶Ϊ1���Ƴ�P��0��1������Q��x��2x��������x2+��2x��1��2=1�����x���ɣ�
��3���������Բ��AC��AB����ʱ���ɵð뾶����Сֵ![]() ��
��
�������Բ������Bʱ���ɵð뾶���ֵ![]() ���ɴ˼��ɽ������.
���ɴ˼��ɽ������.
���������1���١�PQ=![]() ��
��
��S=��r2=5��
������Q��QH��x����H��
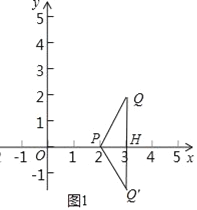
��HQ=![]() =2��
=2��
��Q��������3��2����3����2����
��n=2��2��
��2����ͼ��
��Rt��OAC�У���ACO=30�㣬
��OC=![]() OA=3��
OA=3��
��C��������0��3����
���ABC������Բ��Բ�ĵ�����Ϊ��0��1�����뾶Ϊ1��
��P��0��1����
��Q��x��2x��������x2+��2x��1��2=1��
���x= ![]() ��
��
��Q��![]() ��
�� ![]() ����
����
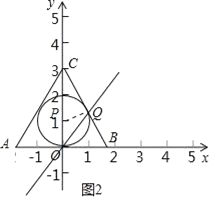
��3����ͼ3�У�

�������Բ��AC��AB����ʱ�뾶����Сֵ![]() ��
��
�������Բ������Bʱ���뾶�����ֵ![]() ��
��
����![]() ��m�ܩ�
��m�ܩ�![]() ��
�� ![]() ��m��
��m��![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�