题目内容
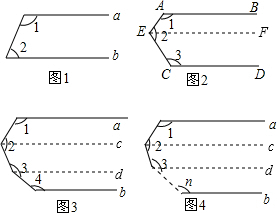
(1)如图1,a∥b,则∠1+∠2=______
(2)如图2,AB∥CD,则∠1+∠2+∠3=______,并说明理由
(3)如图3,a∥b,则∠1+∠2+∠3+∠4=______
(4)如图4,a∥b,根据以上结论,试探究∠1+∠2+∠3+∠4+…+∠n=______(直接写出你的结论,无需说明理由)

 解:(1)∵a∥b,
解:(1)∵a∥b,∴∠1+∠2=180°;
(2)过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠1+∠AEF=180°,
∠CEF+∠2=180°,
∴∠1+∠AEF+∠CEF+∠2=180°+180°,
即∠1+∠2+∠3=360°;
(3)如图,过∠2、∠3的顶点作a的平行线,
则∠1+∠2+∠3+∠4=180°×3=540°;
(4)如图,过∠2、∠3…的顶点作a的平行线,
则∠1+∠2+∠3+∠4+…+∠n=(n-1)•180°.
故答案为:180°;360°;540°;(n-2)•180°.
分析:(1)根据两直线平行,同旁内角互补解答;
(2)过点E作EF∥AB,然后根据两直线平行,同旁内角互补解答;
(3)过∠2、∠3的顶点作a的平行线,然后根据两直线平行,同旁内角互补解答;
(4)过∠2、∠3…的顶点作a的平行线,然后根据两直线平行,同旁内角互补解答.
点评:本题主要考查了两直线平行,同旁内角互补的性质,过拐点作平行线是解题的关键,也是本题的难点.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB=
14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB= 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=

 如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.