Question

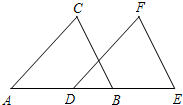
如图，在△ABC中，CE、CF分别平分∠ACB和∠ACD，AE∥CF，AF∥CE，直线EF分别交AB、AC于点M、N．若BC=a，AC=b，AB=c，且c＞a＞b，则ME的长为（　　）

A． c-a 2

B． a-b 2

C． c-b 2

D． a+b-c 2

Answer 1

∵CE、CF分别平分∠ACB和∠ACD，
∴∠ECA=

1

2

∠ACB，∠FCA=

1

2

∠ACD，
∴∠ECF=∠ECA+∠ACF=

1

2

×180°=90°，
∵AE∥CF，AF∥CE，
∴四边形AECF是矩形，
∴AC=EF=b，AN=CN，
∴AM=BM，
∴MN=

1

2

BC=

1

2

a，
∴ME=MN-EN=MN-

1

2

EF=MN-

1

2

AC=

1

2

a-

1

2

b=

a-b

2

．
故选B．