题目内容
如图1,四边形ABCD中,AD⊥AB,AB∥CD,AB=15,AD=12,DC=10,动点P从点C出发,以每秒1个单位的速度向终点D运动;同时动点Q从点出发,以每秒2个单位的速度向终点B运动.连接PQ,设运动时间为t秒.
(1)当t为何值时,四边形CPQB为平行四边形?
(2)如图2所示,若M点是射线AB上的一个动点,且自B点出发,以每秒2个单位的速度向终点向右运动,若M与P、Q同时出发,连接PM,当t为何值时,△PQM为等腰三角形?(请直接写出结果)

(1)当t为何值时,四边形CPQB为平行四边形?
(2)如图2所示,若M点是射线AB上的一个动点,且自B点出发,以每秒2个单位的速度向终点向右运动,若M与P、Q同时出发,连接PM,当t为何值时,△PQM为等腰三角形?(请直接写出结果)

分析:(1)首先根据题意,可用t表示出BQ与CP的长,即可得当BQ=CP时,四边形CPQB为平行四边形,即15-2t=t,解此方程即可求得答案;
(2)首先过P作PE⊥QM于E,即可用t表示出QE与EM的长,然后分别从当PQ=PM时,当PQ=QM时,当PM=QM时,去分析求解即可求得答案.
(2)首先过P作PE⊥QM于E,即可用t表示出QE与EM的长,然后分别从当PQ=PM时,当PQ=QM时,当PM=QM时,去分析求解即可求得答案.
解答:解:(1)根据题意得:CP=t,AQ=2t,
∴BQ=AB-AQ=15-2t,
∵AB∥CD,
∴当BQ=CP时,四边形CPQB为平行四边形,
即15-2t=t,
解得:t=5,
∴当t=5秒时,四边形CPQB是平行四边形;
 (2)过P作PE⊥QM于E,
(2)过P作PE⊥QM于E,
则四边形AEPD是矩形,
∴AE=PE=CD-PC=10-t,
∴QE=AE-AQ=10-3t,
∴EM=15-(10-3t)=3t+5.
①当PQ=PM时,3t+5=10-3t,
解得:t=
;
②当PQ=QM时,(10-3t)2+122=152,
即(10-3t)2=92,
∴10-3t=±9,
解得:t=
或t=
;
③当PM=QM时,(3t+5)2+122=152,
∴(3t+5)2=92,
∴3t+5=±9,
解得:t=
或t=-
(舍);
综上所述:当t=
,
,
,
时,△PQM为等腰三角形.
∴BQ=AB-AQ=15-2t,
∵AB∥CD,
∴当BQ=CP时,四边形CPQB为平行四边形,
即15-2t=t,
解得:t=5,
∴当t=5秒时,四边形CPQB是平行四边形;
 (2)过P作PE⊥QM于E,
(2)过P作PE⊥QM于E,则四边形AEPD是矩形,
∴AE=PE=CD-PC=10-t,
∴QE=AE-AQ=10-3t,
∴EM=15-(10-3t)=3t+5.
①当PQ=PM时,3t+5=10-3t,
解得:t=
| 5 |
| 6 |
②当PQ=QM时,(10-3t)2+122=152,
即(10-3t)2=92,
∴10-3t=±9,
解得:t=
| 1 |
| 3 |
| 19 |
| 3 |
③当PM=QM时,(3t+5)2+122=152,
∴(3t+5)2=92,
∴3t+5=±9,
解得:t=
| 4 |
| 3 |
| 14 |
| 3 |
综上所述:当t=
| 1 |
| 3 |
| 5 |
| 6 |
| 4 |
| 3 |
| 19 |
| 3 |
点评:此题属于四边形的综合题.此题难度较大,涉及了平行四边形的判定与性质、直角梯形的性质以及等腰三角形的性质,注意掌握数形结合思想、分类讨论思想与方程思想的应用.

练习册系列答案
相关题目
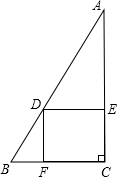 足分别为E、F,得四边形DECF,设DE=x,DF=y.
足分别为E、F,得四边形DECF,设DE=x,DF=y. 如图,AD是△ABC的中线,AE=EF=FC,BE、AD相交于点G,下列4个结论:①DF∥GE;②DF:BG=2:3;③AG=GD;④S△BGD=S四边形EFDG;其中正确的有( )
如图,AD是△ABC的中线,AE=EF=FC,BE、AD相交于点G,下列4个结论:①DF∥GE;②DF:BG=2:3;③AG=GD;④S△BGD=S四边形EFDG;其中正确的有( ) 已知:如图,在四边形ABC中,AD=BC,AB=CD.
已知:如图,在四边形ABC中,AD=BC,AB=CD. 已知:如图,在四边形ABC中,AD=BC,AB=CD.
已知:如图,在四边形ABC中,AD=BC,AB=CD.