题目内容
如图,AB、BC、CD分别与⊙O相切与E,F,G,且AB∥CD,BO=6㎝,CO=8㎝,求BC的长。


10cm.
试题分析:根据切线长定理和平行线的性质定理得到△BOC是直角三角形.再根据勾股定理求出BC的长.
试题解析:∵AB,BC,CD分别与⊙O相切于E,F,G;
∴∠CBO=
 ∠ABC,∠BCO=
∠ABC,∠BCO= ∠DCB,
∠DCB,∵AB∥CD,
∴∠ABC+∠DCB=180°,
∴∠CBO+∠BCO=
 ∠ABC+∠DCB=
∠ABC+∠DCB= (∠ABC+∠DCB)=90°.
(∠ABC+∠DCB)=90°.∴BC=
 cm.
cm.考点: 切割线定理.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目



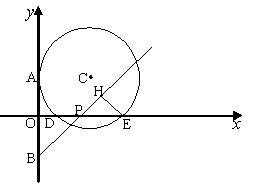

 ,直线AB为⊙O的切线,B为切点.则B点的坐标为__________.
,直线AB为⊙O的切线,B为切点.则B点的坐标为__________.