题目内容
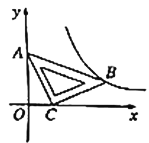
【题目】如右上图，直线l截□ABCD的边AB、BC和对角线BD于P、Q、M，对角线AC、BD
相交于点O，且PB＝3PA，CQ︰BQ＝1︰2，则BM︰BO＝________．
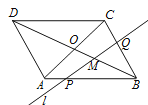
【答案】12:17
【解析】分析：设AE＝2x，利用三角形相似分别把BQ，CQ，DA用x表示，根据△MBQ∽△MDE则可得到BM:MD.
详解：延长AD交直线l于点E，
因为AE∥BQ，所以
，
因为PB＝3PA，所以BQ＝3AE＝6x，
因为CQ:BQ＝1:2，所以CQ＝3x，
因为BC＝BQ＋QC＝6x＋3x＝9x，DE＝AD＋AE＝9x＋2x＝11x.
因为DE∥BQ，所以△MDE∽△MBQ，所以
，
即
，所以
，
所以
，即
，
因为BD＝2OB，所以
，即
.
则
.
故答案为12:17.
练习册系列答案
相关题目
【题目】“十一”黄金周期间，某市在
天中外出旅游的人数变化如下表（正数表示比前一天多的人数，负数表示比前一天少的人数）
日期 |
|
|
|
|
|
|
|
人数变化（万人） |
|
|
|
|
|
|
|
（1）若
月
日外出旅游人数为
，那么
月
日外出旅游的人数是多少？
（2）请判断七天内外出旅游人数最多的是哪天？最少的是哪天？它们相差多少？
（3）如果最多一天有出游人数
万人，那么若月日外出旅游的有多少人？
