题目内容
 如图,已知AD是△ABC的中线,∠ADC=45°,把△ADC绕着点D逆时针旋转45°到△ADE,连接BE,若BC=6cm.
如图,已知AD是△ABC的中线,∠ADC=45°,把△ADC绕着点D逆时针旋转45°到△ADE,连接BE,若BC=6cm.
(1)求BE的长;
(2)求四边形BDAE的面积.
解:(1)∵AD是△ABC的中线,
∴BD=CD= BC=
BC= ×6=3cm,
×6=3cm,
∵∠ADC=45°,△ADC绕着点D逆时针旋转45°到△ADE,
∴AD=BD=DE,∠CDE=45°+45°=90°,
∴△BDE是等腰直角三角形,
∴BE= BD=3
BD=3 cm;
cm;
(2)S四边形BDAE=S△BDE+S△ADE,
= ×3×3+
×3×3+ ×3×(3×
×3×(3× ),
),
=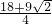 cm2.
cm2.
分析:(1)根据中线定义可得BD=CD,再根据旋转的性质判断出AD=CD,然后求出BD=DE,再根据等腰直角三角形的斜边等于直角边的 倍解答;
倍解答;
(2)根据S四边形BDAE=S△BDE+S△ADE,列式计算即可得解.
点评:本题考查了等腰直角三角形的性质,主要利用了等腰直角三角形的斜边等于直角边的 倍的性质,(2)把四边形的面积分成两个三角形的面积的和求解是解题的关键.
倍的性质,(2)把四边形的面积分成两个三角形的面积的和求解是解题的关键.
∴BD=CD=
 BC=
BC= ×6=3cm,
×6=3cm,∵∠ADC=45°,△ADC绕着点D逆时针旋转45°到△ADE,
∴AD=BD=DE,∠CDE=45°+45°=90°,
∴△BDE是等腰直角三角形,
∴BE=
 BD=3
BD=3 cm;
cm;(2)S四边形BDAE=S△BDE+S△ADE,
=
 ×3×3+
×3×3+ ×3×(3×
×3×(3× ),
),=
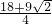 cm2.
cm2.分析:(1)根据中线定义可得BD=CD,再根据旋转的性质判断出AD=CD,然后求出BD=DE,再根据等腰直角三角形的斜边等于直角边的
 倍解答;
倍解答;(2)根据S四边形BDAE=S△BDE+S△ADE,列式计算即可得解.
点评:本题考查了等腰直角三角形的性质,主要利用了等腰直角三角形的斜边等于直角边的
 倍的性质,(2)把四边形的面积分成两个三角形的面积的和求解是解题的关键.
倍的性质,(2)把四边形的面积分成两个三角形的面积的和求解是解题的关键. 
练习册系列答案
相关题目
 9、如图,已知AD是△ABC的角平分线,CE⊥AD,垂足O,CE交AB于E,则下列命题:①AE=AC,②CO=OE,③∠AEO=∠ACO,④∠B=∠ECB.其中正确的是( )
9、如图,已知AD是△ABC的角平分线,CE⊥AD,垂足O,CE交AB于E,则下列命题:①AE=AC,②CO=OE,③∠AEO=∠ACO,④∠B=∠ECB.其中正确的是( ) 18、如图,已知AD是△ABC的角平分线,在不添加任何辅助线的前提下,要使△AED≌△AFD,需添加一个条件是:
18、如图,已知AD是△ABC的角平分线,在不添加任何辅助线的前提下,要使△AED≌△AFD,需添加一个条件是: 如图,已知AD是等腰三角形ABC底边上的高,AD与底边BC的比是2:3,等腰三角形的面积是12cm,求等腰三角形ABC的周长.
如图,已知AD是等腰三角形ABC底边上的高,AD与底边BC的比是2:3,等腰三角形的面积是12cm,求等腰三角形ABC的周长. 如图,已知AD是△ABC的中线,∠ADC=45°,把△ABC沿AD对折,点C落在点E的位置,连接BE,若BC=6cm.
如图,已知AD是△ABC的中线,∠ADC=45°,把△ABC沿AD对折,点C落在点E的位置,连接BE,若BC=6cm. 如图,已知AD是△ABC的角平分线,DE∥AB交AC于点E.那么△ADE是等腰三角形吗?请说明理由.
如图,已知AD是△ABC的角平分线,DE∥AB交AC于点E.那么△ADE是等腰三角形吗?请说明理由.