题目内容

x2•x3=（　　）
A、x5B、x6C、x8D、x9
练习册系列答案
相关题目
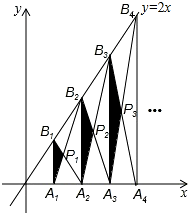如图，已知A1、A2、A3、…、An、An+1是x轴上的点，且OA1=A1A2=A2A3=…=AnAn+1=1，分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1，连接A1B2、B1A2、A2B3、B2A3、…、AnBn+1、BnAn+1，依次相交于点P1、P2、P3、…、Pn．△A1B1P1、△A2B2P2、△AnBnPn的面积依次记为S1、S2、S3、…、Sn，则Sn为（　　）
A、
n+1
2n+1
B、
n2
3n-1
C、
n2
2n-1
D、
n2
2n+1
如图表示甲、乙两车行驶距离与剩余油量的线型关系，其中甲、乙两车均可行驶超过20公里．若甲、乙两车均行驶5公里时，乙车剩余油量比甲车剩余油量多0.5公升，则根据图中的数据，比较甲、乙两车均行驶20公里时的剩余油量，下列叙述何者正确？（　　）
A、甲车剩余油量比乙车剩余油量多1公升B、甲车剩余油量比乙车剩余油量多2公升C、乙车剩余油量比甲车剩余油量多1公升D、乙车剩余油量比甲车剩余油量多2公升
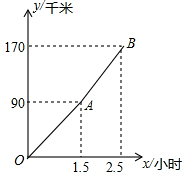“五一节”期间，张老师一家自驾游去了离家170千米的某地，如图是他们离家的距离y（千米）与汽车行驶时间x（小时）之间的函数图象，下面叙述与图象不符的是（　　）
A、他们出发半小时时，离家30千米B、他们出发2小时时，离目的地还有40千米C、后来的速度比开始时提高了20千米/小时D、如果从出发就用AB段的速度行驶，可以提前18分钟到达
如图，在平面直角坐标系中，菱形ABCD的顶点C的坐标为（-1，0），点B的坐标为（0，2），点A在第二象限．直线y=-
1
2
x+5与x轴、y轴分别交于点N、M．将菱形ABCD沿x轴向右平移m个单位，当点D落在△MON的内部时（不包括三角形的边），则m的值可能是（　　）
A、1B、2C、4D、8
在求1+6+62+63+64+65+66+67+68+69的值时，小林发现：从第二个加数起每一个加数都是前一个加数的6倍，于是她设：
S=1+6+62+63+64+65+66+67+68+69①
然后在①式的两边都乘以6，得：
6S=6+62+63+64+65+66+67+68+69+610②
②-①得6S-S=610-1，即5S=610-1，所以S=
610-1
5
，得出答案后，爱动脑筋的小林想：
如果把“6”换成字母“a”（a≠0且a≠1），能否求出1+a+a2+a3+a4+…+a2014的值？你的答案是（　　）
A、
a2014-1
a-1
B、
a2015-1
a-1
C、
a2014-1
a
D、a2014-1
下列计算正确的是（　　）
A、x•x2=x2B、x2•x2=2x2C、x2+x3=x5D、x2•x=x3
下列运算正确的是（　　）
A、3x2+2x3=5x6
B、50=0
C、2-3=
1
6
D、（x3）2=x6
计算下列正确的是（　　）
A、（-a2）3=a6B、a2+a3=a5C、a2•a3=a6D、（-a）3•a2=-a5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网