题目内容
如图，在直角梯形OABD中，DB∥OA，∠OAB=90°，点O为坐标原点，点A在x轴的正半轴上，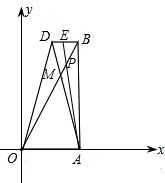
对角线OB，AD相交于点M．OA=2，AB=2| 3 |
（1）求OB和OM的值；
（2）求直线OD所对应的函数关系式；
（3）已知点P在线段OB上（P不与点O，B重合），经过点A和点P的直线交梯形OABD的边于点E（E异于点A），设OP=t，梯形OABD被夹在∠OAE内的部分的面积为S，求S关于t的函数关系式．
分析：（1）由于∠OAB=90°，OA=2，AB=2
，所以OB=4；
因为
=
，所以
=
，OM=
．
（2）由（1）得：OM=
，即BM=
．由于DB∥OA，易证
=
=
，故DB=1，D（1，2
）．故过OD的直线所对应的函数关系式是y=2
x．
（3）依题意：当0＜t≤
时，E在OD边上，分别过E，P作EF⊥OA，PN⊥OA，垂足分别为F和N，由于tan∠PON=
=
，故∠PON=60°，OP=t，故ON=
t，PN=
t，直线OD所对应的函数关系式是y=2
x，
设E（n，2
）易证得△APN∽△AEF，故
=
，故n=
，由此，S△OAE=
OA•EF=
×2×2
×
，
∴S=
（0＜t≤
）；
当
＜t＜4时，点E在BD边上，此时，S梯形OABD=S△ABE+S梯形OAED，
由于DB∥OA，易证：∴△EPB∽△APO，
∴
=
，
∴
=
，BE=
，
可分别求出三角形的值．
| 3 |
因为
| BM |
| OM |
| 1 |
| 2 |
| 4-OM |
| OM |
| 1 |
| 2 |
| 8 |
| 3 |
（2）由（1）得：OM=
| 8 |
| 3 |
| 4 |
| 3 |
| DB |
| OA |
| BM |
| OM |
| 1 |
| 2 |
| 3 |
| 3 |
（3）依题意：当0＜t≤
| 8 |
| 3 |
2
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
设E（n，2
| 3n |
| PN |
| EF |
| AN |
| AF |
| 2t |
| 8-t |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2t |
| 8-t |
∴S=
4
| ||
| 8-t |
| 8 |
| 3 |
当
| 8 |
| 3 |
由于DB∥OA，易证：∴△EPB∽△APO，
∴
| BE |
| OA |
| BP |
| OP |
∴
| BE |
| 2 |
| 4-t |
| t |
| 2(4-t) |
| t |
可分别求出三角形的值．
解答：解：（1）∵∠OAB=90°，OA=2，AB=2
，
∴OB=4，
∵
=
，
∴
=
，
∴OM=
．
（2）由（1）得：OM=
，
∴BM=
，
∵DB∥OA，易证
=
=
，
∴DB=1，D（1，2
），
∴过OD的直线所对应的函数关系式是y=2
x．
（3）依题意：当0＜t≤
时，E在OD边上，
分别过E，P作EF⊥OA，PN⊥OA，垂足分别为F和N，
∵tan∠PON=
=
，∴∠PON=60°，
OP=t．∴ON=
t，PN=
t，
∵直线OD所对应的函数关系式是y=2
x，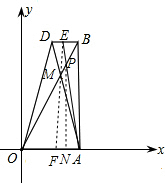
设E（n，2
n）易证得△APN∽△AEF，
∴
=
，
∴
=
，
整理得：
=
，
∴8n-2nt=2t-nt，
∴8n-nt=2t，n（8-t）=2t，
∴n=
．
由此，S△OAE=
OA•EF=
×2×2
×
，
∴S=
（0＜t≤
），
当
＜t＜4时，点E在BD边上，
此时，S梯形OABD=S△ABE+S梯形OAED，
∵DB∥OA，
易证：△EPB∽△APO，
∴
=
，
∴
=
，
BE=
，
S△ABE=
BE•AB=
×
×2
=
×2
=
=
，
∴S=
（1+2）×2
-
×2
=3
-
×2
=-
+5
，
综上所述：S=
．
（3）解法2：①∵∠AOB=90°，OA=2，AB=2
，
易求得：∠ABO=30°，∴OB=4．
解法2：分别过E，P作EF⊥OA，PN⊥OA，垂足分别为F和N，
由①得，∠OBA=30°，
∵OP=t，
∴ON=
t，PN=
t，
即：P（
t，
t），又（2，0），
设经过A，P的直线所对应的函数关系式是y=kx+b，
则
，
解得：k=-
，b=
，
∴经过A，P的直线所对应的函数关系式是y=-
x+
．
依题意：当0＜t≤
时，在OD边上，
∴E（n，2
n），在直线AP上，
∴-
n+
=2
n，
整理得：
-
=2n，
∴n=
，
∴S=
（0＜t≤
），
当
＜t＜4时，点E在BD上，此时，点E坐标是（n，2
），因为E在直线AP上，
∴-
n+
=2
，
整理得：
+
=2∴8n-nt=2t，
∴n=
，
BE=2-n=2-
=
，
∴S=
（1+2）×2
-
×2
=3
-
×2
=-
| 3 |
∴OB=4，
∵
| BM |
| OM |
| 1 |
| 2 |
∴
| 4-OM |
| OM |
| 1 |
| 2 |
∴OM=
| 8 |
| 3 |
（2）由（1）得：OM=
| 8 |
| 3 |
∴BM=
| 4 |
| 3 |
∵DB∥OA，易证
| DB |
| OA |
| BM |
| OM |
| 1 |
| 2 |
∴DB=1，D（1，2
| 3 |
∴过OD的直线所对应的函数关系式是y=2
| 3 |
（3）依题意：当0＜t≤
| 8 |
| 3 |
分别过E，P作EF⊥OA，PN⊥OA，垂足分别为F和N，
∵tan∠PON=
2
| ||
| 2 |
| 3 |
OP=t．∴ON=
| 1 |
| 2 |
| ||
| 2 |
∵直线OD所对应的函数关系式是y=2
| 3 |
设E（n，2
| 3 |
∴
| PN |
| EF |
| AN |
| AF |
∴
| ||||
2
|
2-
| ||
| 2-n |
整理得：
| t |
| 2n |
| 4-t |
| 2-n |
∴8n-2nt=2t-nt，
∴8n-nt=2t，n（8-t）=2t，
∴n=
| 2t |
| 8-t |
由此，S△OAE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2t |
| 8-t |
∴S=
4
| ||
| 8-t |
| 8 |
| 3 |
当
| 8 |
| 3 |
此时，S梯形OABD=S△ABE+S梯形OAED，
∵DB∥OA，
易证：△EPB∽△APO，
∴
| BE |
| OA |
| BP |
| OP |
∴
| BE |
| 2 |
| 4-t |
| t |
BE=
| 2(4-t) |
| t |
S△ABE=
| 1 |
| 2 |
| 1 |
| 2 |
| 2(4-t) |
| t |
| 3 |
| 4-t |
| t |
| 3 |
2
| ||
| t |
8
| ||||
| t |
∴S=
| 1 |
| 2 |
| 3 |
| 4-t |
| t |
| 3 |
| 3 |
| 4-t |
| t |
| 3 |
8
| ||
| t |
| 3 |
综上所述：S=
|
（3）解法2：①∵∠AOB=90°，OA=2，AB=2
| 3 |
易求得：∠ABO=30°，∴OB=4．
解法2：分别过E，P作EF⊥OA，PN⊥OA，垂足分别为F和N，
由①得，∠OBA=30°，
∵OP=t，
∴ON=
| 1 |
| 2 |
| ||
| 2 |
即：P（
| 1 |
| 2 |
| ||
| 2 |
设经过A，P的直线所对应的函数关系式是y=kx+b，
则
|
解得：k=-
| ||
| 4-t |
2
| ||
| 4-t |
∴经过A，P的直线所对应的函数关系式是y=-
| ||
| 4-t |
2
| ||
| 4-t |
依题意：当0＜t≤
| 8 |
| 3 |
∴E（n，2
| 3 |
∴-
| ||
| 4-t |
2
| ||
| 4-t |
| 3 |
整理得：
| tn |
| t-4 |
| 2t |
| t-4 |
∴n=
| 2t |
| 8-t |
∴S=
4
| ||
| 8-t |
| 8 |
| 3 |
当
| 8 |
| 3 |
| 3 |
∴-
| ||
| 4-t |
2
| ||
| 4-t |
| 3 |
整理得：
| tn |
| t-4 |
| 2t |
| t-4 |
∴n=
| 4t-8 |
| t |
BE=2-n=2-
| 4t-8 |
| t |
| 2(4-t) |
| t |
∴S=
| 1 |
| 2 |
| 3 |
| 4-t |
| t |
| 3 |
| 3 |
| 4-t |
| t |
| 3 |
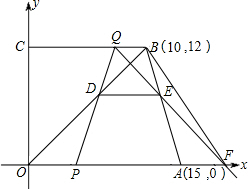动时间为t（单位：秒）．
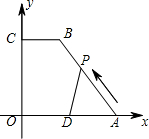（10，0）、C（0，8），CB=4，D为OA中点，动点P自A点出发沿A→B→C→O的线路移动，速度为1个单位/秒，移动时间为t秒．
单位，移动时间记为t秒．
如图，在直角梯形OABC中，AB∥OC，BC⊥x轴于点C，A（1，2），C（3，0）．动点P从O点出发，沿x轴正方向以每秒1个单位长度的速度移动．过P点作PQ⊥直线OA，垂足为Q．设P点移动的时间为t秒（0＜t≤7），△OPQ与直角梯形OABC重叠部分的面积为S．