题目内容
如图,在平面直角坐标系 中,二次函数
中,二次函数 的图象经过点
的图象经过点 ,顶点为
,顶点为 .
.

(1)求这个二次函数的解析式;
(2)若点 的坐标为
的坐标为 ,连接
,连接 ,过点
,过点 作
作 ,垂足为点
,垂足为点 .当点
.当点 在直线
在直线 上,且满足
上,且满足 时,求点
时,求点 的坐标.
的坐标.
 中,二次函数
中,二次函数 的图象经过点
的图象经过点 ,顶点为
,顶点为 .
.
(1)求这个二次函数的解析式;
(2)若点
 的坐标为
的坐标为 ,连接
,连接 ,过点
,过点 作
作 ,垂足为点
,垂足为点 .当点
.当点 在直线
在直线 上,且满足
上,且满足 时,求点
时,求点 的坐标.
的坐标.(1)

(2)点
 的坐标为
的坐标为 或
或
解:(1) 二次函数
二次函数 的图象经过点
的图象经过点 ,
,
 ,得
,得 , …………………………………………1分
, …………………………………………1分
∴二次函数的解析式为 .…………………………………………2分
.…………………………………………2分
(2)由(1)得这个二次函数图象顶点 的坐标为
的坐标为 . ………………………3分
. ………………………3分
如图所示,过点 作
作 轴,垂足为点
轴,垂足为点 .
.

在 中,
中, ,
, ,
, ,
,
 .
.
∵ ,垂足为点
,垂足为点 ,
,
∴ .
.
在 中,
中, ,
,
又 ,
,
可得 .
.
 .
.
有勾股定理得 .
.
过点 作
作 轴,垂足为点
轴,垂足为点 .
.
由题意知,点 在
在 轴的右侧,易证
轴的右侧,易证 .
.
 .
.
设点 的坐标为
的坐标为 ,则
,则 ,
, ,…………………………………4分
,…………………………………4分
①若点 在
在 的延长线上,则
的延长线上,则 .
.
得 ,
,
 ,
, ,
,
所以点 的坐标为
的坐标为 . …………………………………………6分
. …………………………………………6分
②若点 在线段
在线段 上,则
上,则 .
.
得 ,
,
 ,
, ,
,
所以点 的坐标为
的坐标为 .…………………………………………7分
.…………………………………………7分
综上所述,点 的坐标为
的坐标为 或
或 .
.
 二次函数
二次函数 的图象经过点
的图象经过点 ,
, ,得
,得 , …………………………………………1分
, …………………………………………1分∴二次函数的解析式为
 .…………………………………………2分
.…………………………………………2分(2)由(1)得这个二次函数图象顶点
 的坐标为
的坐标为 . ………………………3分
. ………………………3分如图所示,过点
 作
作 轴,垂足为点
轴,垂足为点 .
.
在
 中,
中, ,
, ,
, ,
, .
.∵
 ,垂足为点
,垂足为点 ,
,∴
 .
.在
 中,
中, ,
,又
 ,
,可得
 .
. .
.有勾股定理得
 .
.过点
 作
作 轴,垂足为点
轴,垂足为点 .
.由题意知,点
 在
在 轴的右侧,易证
轴的右侧,易证 .
. .
.设点
 的坐标为
的坐标为 ,则
,则 ,
, ,…………………………………4分
,…………………………………4分①若点
 在
在 的延长线上,则
的延长线上,则 .
.得
 ,
,
 ,
, ,
,所以点
 的坐标为
的坐标为 . …………………………………………6分
. …………………………………………6分②若点
 在线段
在线段 上,则
上,则 .
.得
 ,
, ,
, ,
,所以点
 的坐标为
的坐标为 .…………………………………………7分
.…………………………………………7分综上所述,点
 的坐标为
的坐标为 或
或 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
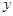 轴对称,则点N的坐标为( ).
轴对称,则点N的坐标为( ).
 (不写
(不写 、
、 在直线
在直线 上,且
上,且 ,则该直线所经过的象限是
,则该直线所经过的象限是