题目内容
 如图,右边有两个边长为4cm的正方形,其中一个正方形的顶点在另一个正方形的中心上,那么图中阴影部分的面积是
如图,右边有两个边长为4cm的正方形,其中一个正方形的顶点在另一个正方形的中心上,那么图中阴影部分的面积是4cm2
4cm2
.分析:如图点O是正方形的中心,连接OA、OB,就可以证明△BOD≌△AOC,就可以得到四边形ACOB的面积=△AOB的面积,求出三角形AOB的面积就可以了.
解答: 解:如图,设点O是正方形的中心,连接OA、OB,
解:如图,设点O是正方形的中心,连接OA、OB,
∴OA=OB,∠AOB=90°.
∴∠OAB=∠OBA=45°
∴∠OAC=45°,
∴∠OAC=∠OBD
∵AB=4,在Rt△AOB中,由勾股定理得:
AO=BO=2
,
∴S△AOB=
=4.
∵∠BOC=90°,
∴∠BOC=∠AOB,
∴∠1=∠2.
在△AOC和△BOD中,
∵
,
∴△AOC≌△BOD,
∴S△AOC=S△BOD,
∴S四边形ACOD=S△AOB,
∴S四边形ACOD=4cm2.
故答案为:4cm2.
 解:如图,设点O是正方形的中心,连接OA、OB,
解:如图,设点O是正方形的中心,连接OA、OB,∴OA=OB,∠AOB=90°.
∴∠OAB=∠OBA=45°
∴∠OAC=45°,
∴∠OAC=∠OBD
∵AB=4,在Rt△AOB中,由勾股定理得:
AO=BO=2
| 2 |
∴S△AOB=
2
| ||||
| 2 |
∵∠BOC=90°,
∴∠BOC=∠AOB,
∴∠1=∠2.
在△AOC和△BOD中,
∵
|
∴△AOC≌△BOD,
∴S△AOC=S△BOD,
∴S四边形ACOD=S△AOB,
∴S四边形ACOD=4cm2.
故答案为:4cm2.
点评:本题考查了正方形的性质,勾股定理的运用,三角形的面积公式的运用,全等三角形的判定及性质.在解答中灵活运用图形转化是关键.

练习册系列答案
相关题目

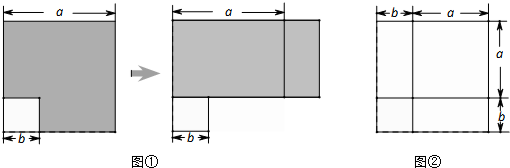
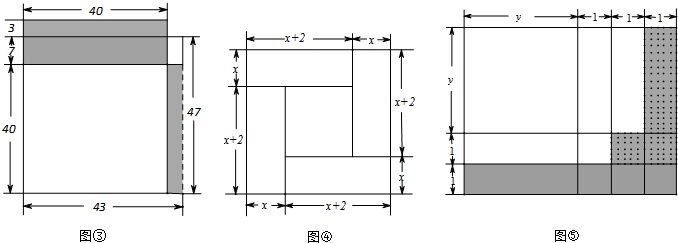
 如图,右边有两个边长为4cm的正方形,其中一个正方形的顶点在另一个正方形的中心上,那么图中阴影部分的面积是________.
如图,右边有两个边长为4cm的正方形,其中一个正方形的顶点在另一个正方形的中心上,那么图中阴影部分的面积是________. 如图,右边有两个边长为4cm的正方形,其中一个正方形的顶点在另一个正方形的中心上,那么图中阴影部分的面积是 .
如图,右边有两个边长为4cm的正方形,其中一个正方形的顶点在另一个正方形的中心上,那么图中阴影部分的面积是 .