题目内容
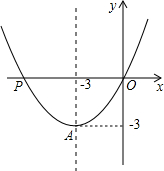已知抛物线y=ax2+bx经过点A（-3，-3）和点P（t，0），且t≠0．
（1）若t=-4，求抛物线的解析式，并指出此时抛物线的开口方向；
（2）如图，抛物线y=ax2+bx的对称轴经过点A，观察图象并回答：
y的最小值=______；
t的值=______；
当x＞-3时，y随x的增大而______．
解：（1）根据题意得：
，
解得：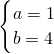
，
则抛物线的解析式是：y=x2+4x；
（2）根据图象可以得到y的最小值是-3；
点P与原点关于x=-3对称，则P的坐标是（-6，0），故t=-6；
当x＞-3时，y随x的增大而增大．
故答案是：-3，-6，增大．
分析：（1）利用待定系数即可求得函数的解析式；
（2）根据函数的图象即可写出．
点评：本题考查了用待定系数法求函数解析式的方法，同时还考查了方程组的解法等知识，难度不大．
，解得：
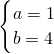，则抛物线的解析式是：y=x2+4x；
（2）根据图象可以得到y的最小值是-3；
点P与原点关于x=-3对称，则P的坐标是（-6，0），故t=-6；
当x＞-3时，y随x的增大而增大．
故答案是：-3，-6，增大．
分析：（1）利用待定系数即可求得函数的解析式；
（2）根据函数的图象即可写出．
点评：本题考查了用待定系数法求函数解析式的方法，同时还考查了方程组的解法等知识，难度不大．
练习册系列答案
名校课堂系列答案
相关题目
与x轴的另一个交点为E．
如图，已知抛物线y=ax2+bx+c（其中b＞0，c＜0）的顶点P在x轴上，与y轴交于点Q，过坐标原点O，作OA⊥PQ，垂足为A，且OA=