题目内容
 等腰梯形ABCD中,AB∥CD,AD=BC=10,AB=16,∠B=60°,P是边AB上的一点,设PB=a,过P作PM⊥BC于M,把△PBM沿PM折叠,折痕为PM,折叠后△PBM与五边形APMCD的重叠部分的面积用含a的代数式表示为
等腰梯形ABCD中,AB∥CD,AD=BC=10,AB=16,∠B=60°,P是边AB上的一点,设PB=a,过P作PM⊥BC于M,把△PBM沿PM折叠,折痕为PM,折叠后△PBM与五边形APMCD的重叠部分的面积用含a的代数式表示为分析:本题△PBM折叠后与五边形APMCD的重叠部分的面积,存在两种情况,当0≤a≤10时,重叠部分的面积就是PBM的面积,当10<a≤16时,重叠部分的面积等于△ABM的面积-△ECF的面积.分两种情况分别计算就可以了.
解答: 解:∵AB∥CD,
解:∵AB∥CD,
∴∠B=∠ECD=60°,
∴∠E=∠ECD=60°,
∵PM⊥BC,
∴∠PMB=∠PMC=90°,
∴∠MPB=30°,
∴MB=
BP=
a,
在Rt△PBM中由勾股定理,得
PM=
a,
∴当0≤a≤10时,
重叠部分的面积为:
=
a2,
当10<a≤16时,重叠部分的面积为:
S△PME-S△CEF=
-
=-
a2+5
a-25
,
故答案为:
a2或-
a2+5
a-25
.
 解:∵AB∥CD,
解:∵AB∥CD,∴∠B=∠ECD=60°,
∴∠E=∠ECD=60°,
∵PM⊥BC,
∴∠PMB=∠PMC=90°,
∴∠MPB=30°,
∴MB=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△PBM中由勾股定理,得
PM=
| ||
| 2 |
∴当0≤a≤10时,
重叠部分的面积为:
| ||||||
| 2 |
| ||
| 8 |
当10<a≤16时,重叠部分的面积为:
S△PME-S△CEF=
| ||||||
| 2 |
(
| ||||||
| 2 |
=-
| ||
| 8 |
| 3 |
| 3 |
故答案为:
| ||
| 8 |
| ||
| 8 |
| 3 |
| 3 |
点评:本题是一道折叠为题的几何解答题,考查了直角三角形的性质:30°所对的直角边等于斜边的一半,勾股定理的运用,轴对称的性质及等腰梯形的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

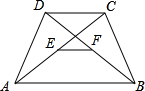 如图,在等腰梯形ABCD中,AB∥CD,∠ABC=60°,AC平分∠DAB,E、F分别为对角线AC、DB的中点,且EF=4.求这个梯形的面积.
如图,在等腰梯形ABCD中,AB∥CD,∠ABC=60°,AC平分∠DAB,E、F分别为对角线AC、DB的中点,且EF=4.求这个梯形的面积. (1)如图,在等腰梯形ABCD中,AD∥BC,AB∥DE,BC=8,AD=5,求EC的长.
(1)如图,在等腰梯形ABCD中,AD∥BC,AB∥DE,BC=8,AD=5,求EC的长.
 在等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠C=60°,
在等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠C=60°, 等腰梯形ABCD中,AD=2,BC=4,高DF=2,则腰CD长是
等腰梯形ABCD中,AD=2,BC=4,高DF=2,则腰CD长是