Question

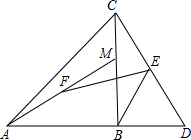（2012•萧山区一模）如图，△ABC中，∠ABC=Rt∠，AB=BC，点M是BC边上任意一点，点D是AB的延长线上一点，且BM=BD；又点E、F分别是CD、AM边上的中点，连接FE、EB．
（1）求证：△AMB≌△CDB；
（2）点M在BC边上移动时，试问∠BEF的度数是否会发生变化？若不变，请求出∠BEF的度数；若变化，请说明理由；
（3）若

EF

AC

=

3

5

，且设∠MAB=α，试求cosα的值．

Answer 1

分析：（1）求出∠ABM=∠CBD，根据SAS推出全等即可；
（2）根据全等求出AM=DC，推出BE=BF，求出∠EBF=90°，即可得出∠BEF=45°；
（3）设EF=3a，AC=5a，由勾股定理求出AB=BC=

5 2

2

a，BF=BE=

3 2

2

a，求出AM=2BF=3

2

a，解直角三角形求出即可．

解答：（1）证明：∵∠ABC=90°，
∴∠ABM=∠CBD=90°，
∵在△AMB和△CDB中

AB=BC ∠ABM=∠CBD BM=BD

，
∴△AMB≌△CDB（SAS）；

（2）解：∠BEF的度数不发生变化，
理由是：连接BF，
∵△AMB≌△CDB，
∴∠DCB=∠MAB，AM=DC，
∵E、F分别为DC、AM中点，∠ABM=∠CBD=90°，
∴BE=DE=CE

1

2

CD，BF=MF=AF=

1

2

AM，
∴BE=BF，∠BAF=∠FBA，∠EBD=∠D，
∵∠D+∠DCB=90°，
∴∠FBA+∠EBD=90，
∴∠FBE=180°-90°=90°，
∵BE=BF，
∴∠BEF=45°；

（3）解：设EF=3a，AC=5a，
∵∠ABC=90°，AB=BC，
∴由勾股定理得：AB=BC=

5 2

2

a，
同理：BF=BE=

3 2

2

a，
∴AM=2BF=3

2

a，
∴cosα=cos∠MAB=

AB

AM

=

5 2 2 a

3 2 a

=

5

6

．

点评：本题考查了等腰直角三角形性质和判定，直角三角形斜边上中线，全等三角形的性质和判定，解直角三角形，勾股定理的应用，关键是推出△AMB≌△CDB和求出△EBF是等腰直角三角形．