题目内容
如图,以半圆的一条弦BC为对称轴将弧BC折叠后与直径AB交于点D,若AD=4,BD=8,则CB的长为

 .
.
【解析】
试题分析:根据折叠的性质可得 ,再根据在同圆或等圆中,等弧所对的圆周角相等可得∠BAC=∠BCD+∠CBD,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ADC=∠BCD+∠CBD,从而得到∠BAC=∠ADC,根据等角对等边可得AC=CD,过点C作CE⊥AD于E,根据等腰三角形三线合一的性质可得AE=DE=
,再根据在同圆或等圆中,等弧所对的圆周角相等可得∠BAC=∠BCD+∠CBD,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ADC=∠BCD+∠CBD,从而得到∠BAC=∠ADC,根据等角对等边可得AC=CD,过点C作CE⊥AD于E,根据等腰三角形三线合一的性质可得AE=DE= AD,然后利用△ACE和△CBE相似,根据相似三角形对应边成比例列式求出CE,在Rt△BCE中,利用勾股定理列式计算即可得解.
AD,然后利用△ACE和△CBE相似,根据相似三角形对应边成比例列式求出CE,在Rt△BCE中,利用勾股定理列式计算即可得解.
试题解析:∵弧BC沿弦BC折叠交直径AB于点D,
∴ ,
,
∴∠BAC=∠BCD+∠CBD,
在△BCD中,∠ADC=∠BCD+∠CBD,
∴∠BAC=∠ADC,
∴AC=CD,
过点C作CE⊥AD于E,

则AE=DE= AD=
AD= ×4=2,
×4=2,
∴BE=BD+DE=8+2=10,
∵AB是直径,
∴∠ACB=90°,
∴∠ACE+∠BCE=∠ACB=90°,
∵∠ACE+∠CAE=180°-90°=90°,
∴∠CAE=∠BCE,
又∵∠AEC=∠BEC=90°,
∴△ACE∽△CBE,
∴ ,
,
∴CE= ,
,
在Rt△BCE中,BC= =
= .
.
考点:1.翻折变换(折叠问题);2.勾股定理;3.垂径定理.

练习册系列答案
相关题目
 -(
-( )-1-
)-1-
 。其中x=
。其中x=
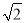 ,⊙O的半径为1,P是AB边上的动点,过点P作⊙O的切线PQ,切点为Q,则切线长PQ的最小值为
,⊙O的半径为1,P是AB边上的动点,过点P作⊙O的切线PQ,切点为Q,则切线长PQ的最小值为 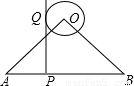

 中,函数y与自变量x的部分对应值如下表:
中,函数y与自变量x的部分对应值如下表: