题目内容
（2008•乐山）如图，在直角梯形ABCD中AD∥BC，点E是边CD的中点，若AB=AD+BC，BE=
，则梯形ABCD的面积为（ ）
A．
B．
C．
D．25
【答案】分析：此题的关键是作辅助线，求出AB的值，然后求出梯形的面积．
解答：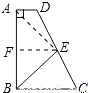
解：连AE，过E作EF∥BC交AB于点F，
∵E为CD的中点，
∴EF平分AB，EF是梯形ABCD的中位线，
故EF=
（AD+BC），
又∵BC⊥AB，
∴EF是AB的垂直平分线，根据垂径定理得：AE=BE=
∵AB=AD+BC，EF=
（AD+BC）=
AB，∴△ABE是等腰直角三角形．
由勾股定理得：AB=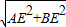
=
=
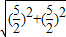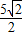，即AD+BC=
，
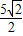S梯形ABCD=
（AD+BC）•AB
=
（AD+BC）（AD+BC）
=
×
×
=
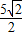
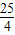
故选A．
点评：本题属中等难度，解答此题的关键是连AE，过E作EF∥BC，利用梯形的中位线定理，垂径定理证明△ABE是等腰直角三角形，再利用梯形的面积公式求解．
解答：
解：连AE，过E作EF∥BC交AB于点F，∵E为CD的中点，
∴EF平分AB，EF是梯形ABCD的中位线，
故EF=
（AD+BC），又∵BC⊥AB，
∴EF是AB的垂直平分线，根据垂径定理得：AE=BE=
∵AB=AD+BC，EF=
（AD+BC）=AB，∴△ABE是等腰直角三角形．由勾股定理得：AB=
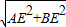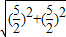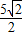==，即AD+BC=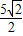，S梯形ABCD=
（AD+BC）•AB=
（AD+BC）（AD+BC）=
××=
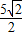
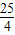
故选A．
点评：本题属中等难度，解答此题的关键是连AE，过E作EF∥BC，利用梯形的中位线定理，垂径定理证明△ABE是等腰直角三角形，再利用梯形的面积公式求解．
练习册系列答案
相关题目
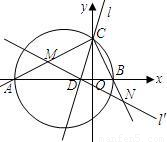
的是否为定值？若是，求出该定值；若不是，请说明理由．
的是否为定值？若是，求出该定值；若不是，请说明理由．
