题目内容
某电信公司有甲、乙两种手机收费业务.甲种业务规定月租费25元,另外每通话1分钟收费0.4元;乙种业务不收月租费,但每通话1分钟收费0.6元.试问选择哪种业务对顾客更合算?
考点:一元一次方程的应用
专题:
分析:分别根据两种收费标准得出y与x的函数关系即可;利用所求关系式首先得出费用一样时通话时间进而得出合适的收费方式.
解答:解:∵甲种业务的收费标准是月租费50元,每1分钟收费0.4元;乙种业务的收费标准是没有月租费,但每分钟收费0.6元.
∴甲、乙两种业务每月应缴费用y(元)与通话时间x(分)之间的关系式分别为:y=50+0.4x,y=0.6x;
当50+0.4x=0.6x,
解得:x=250,
即当通话时间为250分钟两种方式收费一样,当超过250分钟时,选择甲方式省钱,当小于250分钟时,选择乙方式省钱.
∴甲、乙两种业务每月应缴费用y(元)与通话时间x(分)之间的关系式分别为:y=50+0.4x,y=0.6x;
当50+0.4x=0.6x,
解得:x=250,
即当通话时间为250分钟两种方式收费一样,当超过250分钟时,选择甲方式省钱,当小于250分钟时,选择乙方式省钱.
点评:此题主要考查了一次函数的应用,根据已知得出两种收费的函数关系式是解题关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
一艘轮船在两个码头间航行,顺水需要6小时到达,逆水需要7小时到达,已知水流速度是每小时2千米,设码头间的距离为x千米,则可列出方程是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列各组代数式中,不是同类项的一组是( )
| A、5x2y和-yx2 | ||
| B、-32和3 | ||
| C、x2y和2xy2 | ||
D、3xy和-
|
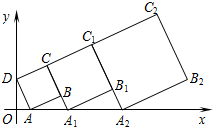 在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2014个正方形的面积为
在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2014个正方形的面积为