题目内容
 如图,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,sinA=
如图,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,sinA= ,则下列结论:①DE=3cm;②EB=1cm;③S菱形ABCD=7.5cm2;④cos∠CDB=
,则下列结论:①DE=3cm;②EB=1cm;③S菱形ABCD=7.5cm2;④cos∠CDB= .其中正确结论的个数有
.其中正确结论的个数有
- A.4个
- B.3个
- C.2个
- D.1个
B
分析:根据菱形的周长可以求得菱形的边长,再根据解直角三角形的知识求得DE的长,进而求得BE的长;根据平行四边形的面积等于底×高计算该菱形的面积;根据勾股定理求得BD的长,从而求得cos∠DBE,即为cos∠CDB的值.
解答:根据题意,得菱形的边长是5cm.
①在直角三角形ADE中,sinA= ,∴DE=5×
,∴DE=5× =3(cm),故此选项正确;
=3(cm),故此选项正确;
②在直角三角形ADE中,根据勾股定理,得AE=4,则BE=5-4=1(cm),故此选项正确;
C、根据菱形的面积等于底×高,则菱形的面积是5×3=15(cm2),故此选项错误;
D、∵AB∥CD,∴∠CDB=∠DBE.在直角三角形BDE中,根据勾股定理,得BD= =
= ,∴cos∠CDB=
,∴cos∠CDB= .故此选项正确.
.故此选项正确.
故选B.
点评:此题综合运用了解直角三角形的知识、勾股定理和平行四边形的面积公式.
分析:根据菱形的周长可以求得菱形的边长,再根据解直角三角形的知识求得DE的长,进而求得BE的长;根据平行四边形的面积等于底×高计算该菱形的面积;根据勾股定理求得BD的长,从而求得cos∠DBE,即为cos∠CDB的值.
解答:根据题意,得菱形的边长是5cm.
①在直角三角形ADE中,sinA=
 ,∴DE=5×
,∴DE=5× =3(cm),故此选项正确;
=3(cm),故此选项正确;②在直角三角形ADE中,根据勾股定理,得AE=4,则BE=5-4=1(cm),故此选项正确;
C、根据菱形的面积等于底×高,则菱形的面积是5×3=15(cm2),故此选项错误;
D、∵AB∥CD,∴∠CDB=∠DBE.在直角三角形BDE中,根据勾股定理,得BD=
 =
= ,∴cos∠CDB=
,∴cos∠CDB= .故此选项正确.
.故此选项正确.故选B.
点评:此题综合运用了解直角三角形的知识、勾股定理和平行四边形的面积公式.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
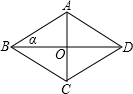 如图,菱形ABCD的对角线AC=6,BD=8,∠ABD=α,则下列结论正确的是( )
如图,菱形ABCD的对角线AC=6,BD=8,∠ABD=α,则下列结论正确的是( )A、sinα=
| ||
B、cosα=
| ||
C、tanα=
| ||
D、tanα=
|
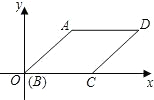 如图,菱形ABCD的边长为2,∠ABC=45°,则点D的坐标为
如图,菱形ABCD的边长为2,∠ABC=45°,则点D的坐标为 如图,菱形ABCD的边长为6且∠DAB=60°,以点A为原点、边AB所在的直线为x轴且顶点D在第一象限建立平面直角坐标系.动点P从点D出发沿折线DCB向终点B以2单位/每秒的速度运动,同时动点Q从点A出发沿x轴负半轴以1单位/秒的速度运动,当点P到达终点时停止运动,运动时间为t,直线PQ交边AD于点E.
如图,菱形ABCD的边长为6且∠DAB=60°,以点A为原点、边AB所在的直线为x轴且顶点D在第一象限建立平面直角坐标系.动点P从点D出发沿折线DCB向终点B以2单位/每秒的速度运动,同时动点Q从点A出发沿x轴负半轴以1单位/秒的速度运动,当点P到达终点时停止运动,运动时间为t,直线PQ交边AD于点E. △ABC重叠部分的面积为ycm2(规定:点和线段是面积为0的三角形).
△ABC重叠部分的面积为ycm2(规定:点和线段是面积为0的三角形).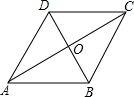 已知:如图,菱形ABCD的周长为8cm,∠ABC:∠BAD=2:1,对角线AC、BD相交于点O,求BD及AC的长.
已知:如图,菱形ABCD的周长为8cm,∠ABC:∠BAD=2:1,对角线AC、BD相交于点O,求BD及AC的长.