题目内容
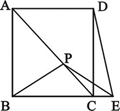
如图,正方形ABCD中,P是AC上一点,E是BC延长线上一点,且PB=PE.若BP=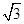 ,求DE的长.
,求DE的长.
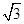 ,求DE的长.
,求DE的长.

试题分析:连接DP,根据正方形的性质可得∠PDC=∠PBC,PB=PD,再根据等边对等角可得∠PBC=∠PEB,然后求出∠DPE=∠DCE=90°,再利用勾股定理列式计算即可得解.
如图,连接DP,

在正方形ABCD中,∠PDC=∠PBC,PB=PD,
∵PB=PE,
∴∠PBC=∠PEB,
∴∠PBC=∠PEB=∠PDC,
∵∠1=∠2(对顶角相等),
∴∠DPE=∠DCE=90°,
∵BP=PE=
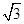 ,
,∴DE=
 .
.
练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
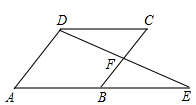

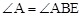 .若
.若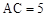 ,
,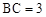 ,则BD的长为( )
,则BD的长为( )