Question

如图1，在平面直角坐标系xOy中，点M在x轴的正半轴上，⊙M交x轴于A、B两点，交y轴于C、D两点，且C为

AE

的中点，AE交y轴于G点，若点A的坐标为（-2，0），AE=8．

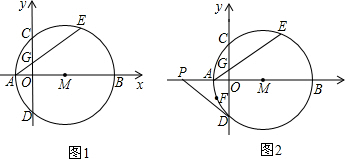
（1）求点C的坐标；
（2）连接MG、BC，求证：MG∥BC；
（3）如图2，过点D作⊙M的切线，交x轴于点P．动点F在⊙M的圆周上运动时，

OF

PF

的比值是否发生变化？若不变，求出比值；若变化，说明变化规律．

Answer 1

分析：（1）求C点的坐标，即求出OC的长．根据垂径定理可得出弧CD=2弧AC，而题中已经告诉了C是弧AE的中点，即弧AE=2弧AC，即弧CD=弧AE，因此CD=AE，那么OC=

1

2

AE=4，即可求出C点坐标；
（2）由于无法直接证明∠OMG=∠OBC来得出两直线平行，因此可通过相似三角形来求解，可设出圆的半径，然后分别求出OG、OM、OB的长，然后通过证OG、OM，OC、OB对应成比例来得出△OMG与△OBC相似来得出∠OMG=∠OBC，进行得出所求的结论；
（3）OF与OP的比例关系不变，在直角三角形DMP中，根据射影定理有DM²=MO•MP，①同理可求出OD²=OM•OP；
②然后分三种情况：
A：F与A重合时，OF=OA，PF=PA，可根据②求出OP的长根据①求出MP的长即可求出OP的长，进而可求出所求的比例关系；
B：F与B重合，同一；
C：F不与A、B重合．可通过相似三角形来求解．由于MF=DM，根据①可得出△OMF与△FMP相似，可得出

OF

PF

=

OM

MF

=

OM

MA

．
综合三种情况即可得出OF：PF的值．

解答：（1）解：方法（一）
∵直径AB⊥CD，
∴CO=

1

2

CD，

AD

=

AC

，
∵C为

AE

的中点，
∴

AC

=

CE

，
∴

AE

=

CD

，
∴CD=AE，
∴CO=

1

2

CD=4，
∴C点的坐标为（0，4）．
方法（二）如图1，连接BG，GM，连接CM，交AE于点N，
∵C为

AE

的中点，M为圆心，
∴AN=

1

2

AE=4，
CM⊥AE，
∴∠ANM=∠COM=90°，
在△ANM和△COM中：
∵

∠CMO=∠AMN ∠ANM=∠COM AM=CM

，
∴△ANM≌△COM（AAS），
∴CO=AN=4，
∴C点的坐标为（0，4）．

（2）证明：设半径AM=CM=r，则OM=r-2，
由OC²+OM²=MC²得：
4²+（r-2）²=r²，
解得：r=5，（1分）
∴OM=r-OA=3
∵∠AOC=∠ANM=90°，
∠EAM=∠MAE，
∴△AOG∽△ANM，
∴

OG

MN

=

AO

AN

，
∵MN=OM=3，
即

OG

3

=

2

4

，
∴OG=

3

2

，（2分）
∵

OG

OC

=

1.5

4

=

3

8

，

OM

OB

=

3

8

，
∴

OG

OC

=

OM

OB

，
∵∠BOC=∠BOC，
∴△GOM∽△COB，
∴∠GMO=∠CBO，
∴MG∥BC．

（3）解：如图2，连接DM，则DM⊥PD，DO⊥PM，
∴△MOD∽△MDP，△MOD∽△DOP，
∴DM²=MO•MP；
DO²=OM•OP，
即4²=3•OP，
∴OP=

16

3

．
当点F与点A重合时：

OF

PF

=

AO

AP

=

2

16 3 -2

=

3

5

，
当点F与点B重合时：

OF

PF

=

OB

PB

=

8

16 3 +8

=

3

5

，
当点F不与点A、B重合时：连接OF、PF、MF，
∵DM²=MO•MP，
∴FM²=MO•MP，
∴

FM

OM

=

MP

FM

，
∵∠AMF=∠FMA，
∴△MFO∽△MPF，
∴

OF

PF

=

MO

MF

=

3

5

．
∴综上所述，

OF

PF

的比值不变，比值为

3

5

．

点评：命题立意：考查坐标系和圆的有关知识．