题目内容
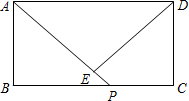 如图,在长方形ABCD中,AB=6,BC=8,P是BC边上一动点,过D作DE⊥AP于E,设AP=x,DE=y,试求出y与x之间的函数关系式,并画出函数图象.
如图,在长方形ABCD中,AB=6,BC=8,P是BC边上一动点,过D作DE⊥AP于E,设AP=x,DE=y,试求出y与x之间的函数关系式,并画出函数图象.
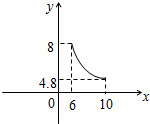 解:∵四边形ABCD是长方形,
解:∵四边形ABCD是长方形,∴AD∥BC,∠ABP=90°,
∴∠DAE=∠APB,
又∵DE⊥AP,
∴∠AED=90°,
∴∠ABP=∠AED,
∴△ABP∽△DEA,
∴
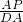 =
=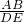 ,
,∴
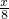 =
=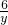 ,
,∴xy=48,
∴
 (6≤x≤10).
(6≤x≤10).函数图象如图所示:
分析:首先能得出∠ABP=∠AED=90°,因为四边形ABCD是长方形,那么AD∥BC,根据内错角相等,两直线平行可得出一对内错角相等,故可证△ABP∽△DEA.根据相似三角形对应边成比例,就可得出y与x之间的函数关系式.
点评:本题考查了矩形的性质以及相似三角形的判定和相似三角形的性质,题目难度不大,具有一定的综合性.

练习册系列答案
相关题目
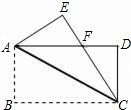 于点F.
于点F. 如图,在Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,以D作DE⊥AC与CB的延长线交于E,以AB、BE为邻边作长方形ABEF,连接DF,求DF的长.
如图,在Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,以D作DE⊥AC与CB的延长线交于E,以AB、BE为邻边作长方形ABEF,连接DF,求DF的长.

