题目内容
13.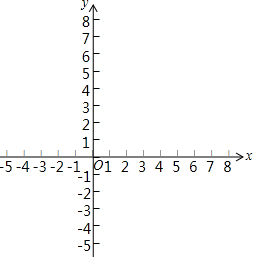 填上表格画出函数y=x2-2x-3的图象,并利用图象回答:
填上表格画出函数y=x2-2x-3的图象,并利用图象回答:(1)方程x2-2x-3=0的解是什么;
(2)x取什么值时,函数值大于0;
(3)x取什么值时,函数值小于0.
列表:
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y=x2-2x-3 | … | … |
分析 根据解析式计算、填表,然后在坐标系内描点、连线画出图象,根据图象信息进行解答即可.
解答 解:填表如下:
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y=x2-2x-3 | … | 5 | 0 | -3 | -4 | -3 | 0 | 5 | … |

(1)方程x2-2x-3=0的解是x1=-1,x2=3,
(2)x<-1或x>3时,函数值大于0,
(3)-1<x<3时,函数值小于0.
点评 本题考查的是用列表法画函数图象、根据图象求一元二次方程的解和不等式的解集,读懂函数图象,从中获取正确的信息是解题的关键,画图象时,要按照列表、描点、连线的步骤进行.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
2.正六边形半径为R,则它的边长、边心距、面积分别为( )
| A. | $\frac{2\sqrt{3}}{3}$R,R,$\sqrt{3}$R2 | B. | R,$\frac{R}{2}$,2$\sqrt{3}$R2 | C. | $\frac{\sqrt{3}}{3}$R,R,2$\sqrt{3}$R2 | D. | R,$\frac{\sqrt{3}}{2}$R,$\frac{{3\sqrt{3}}}{2}{R^2}$ |
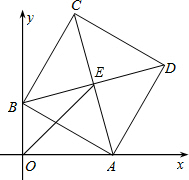 已知边长为a的正方形ABCD,两顶点A、B分别在平面直角坐标系的x轴、y轴的正半轴上滑动,点C点D在第一象限,点E为正方形ABCD的对称中心,连结OE,则OE的长的最大值是a.
已知边长为a的正方形ABCD,两顶点A、B分别在平面直角坐标系的x轴、y轴的正半轴上滑动,点C点D在第一象限,点E为正方形ABCD的对称中心,连结OE,则OE的长的最大值是a.