题目内容
如图,延长梯形ABCD两腰DA和CB交于点P,两对角线AC和BD交于点Q,△PAB和△QBC的面积分别是20和6,则△PCD的面积是分析:首先由AB∥CD,△QBC的面积为6,得到△QAD的面积也为6,然后设△ABQ的面积为x,△CDQ的面积为y,根据相似三角形的性质可得:
=
=
,又由△ABP与△ABC还有△DBP与△DBC的关系,可得:
=
,则可求得x与y的值,即可求得答案.
| 6 |
| x |
| y |
| 6 |
| AQ |
| CQ |
| 20 |
| x+6 |
| 20+x+6 |
| 6+y |
解答:解:∵AB∥CD,△QBC的面积为6,
∴△QAD的面积也为6,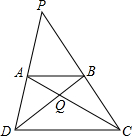
设△ABQ的面积为x,△CDQ的面积为y,
∵
=
=
,
∴xy=36,
∵
=
,
=
,
∴
=
,
∴
=
=
=
=
,
∴x2+26x-120=0,
∴x1=4,x2=-30(不合题意,舍去),
∴x=4,
则:y=9,
∴△PCD的面积为:20+6+6+x+y=45.
故答案为:45.
∴△QAD的面积也为6,

设△ABQ的面积为x,△CDQ的面积为y,
∵
| 6 |
| x |
| y |
| 6 |
| AQ |
| CQ |
∴xy=36,
∵
| S△ABP |
| S△ABC |
| PB |
| BC |
| S△DBP |
| S△DBC |
| PB |
| BC |
∴
| 20 |
| x+6 |
| 20+x+6 |
| 6+y |
∴
| 20 |
| x+6 |
| 20+x+6-20 |
| 6+y-(x+6) |
| x+6 |
| y-x |
| x(x+6) |
| 36-x2 |
| x |
| 6-x |
∴x2+26x-120=0,
∴x1=4,x2=-30(不合题意,舍去),
∴x=4,
则:y=9,
∴△PCD的面积为:20+6+6+x+y=45.
故答案为:45.
点评:此题考查了相似三角形的性质以及等高三角形面积的比等于其对应底的比的知识.解此题的关键是要注意数形结合思想与方程思想的应用.

练习册系列答案
 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2,过点D作DE∥AB,交∠BCD的平分线于点E,连接BE.
如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2,过点D作DE∥AB,交∠BCD的平分线于点E,连接BE.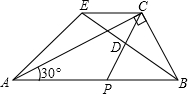 如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=4,点P是斜边AB上一个动点,点D是CP的中点,延长BD至E,使DE=BD,连接AE.
如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=4,点P是斜边AB上一个动点,点D是CP的中点,延长BD至E,使DE=BD,连接AE.
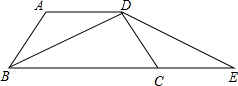 如图,在梯形ABCD中,AD∥BC,AB=DC=1,BD平分∠ABC,BD⊥CD.
如图,在梯形ABCD中,AD∥BC,AB=DC=1,BD平分∠ABC,BD⊥CD. 如图,在梯形ABCD中,AD∥BC,AB=CD,延长CB到E,使EB=AD,连接AE.
如图,在梯形ABCD中,AD∥BC,AB=CD,延长CB到E,使EB=AD,连接AE.