题目内容
解方程: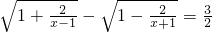
解:原方程可化为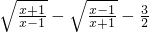 =0.
=0.
设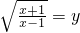 ,则原方程变为y-
,则原方程变为y- -
- =0,
=0,
整理,得2y2-3y-2=0.
解得y1=- ,y2=2
,y2=2
当y=- 时,原方程无解.
时,原方程无解.
当y=2时, =4,∴x=
=4,∴x=
经检验x= 是原方程的根
是原方程的根
∴原方程的根为x=
分析:原方程中的根式分别通分后,设 =y,需要注意的是用来换元的式子为设
=y,需要注意的是用来换元的式子为设 ,则2y2-3y-2=0.
,则2y2-3y-2=0.
点评:在解无理方程时最常用的方法是换元法,一般方法是通过观察确定用来换元的式子,例如本题中的 =y.
=y.
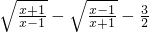 =0.
=0.设
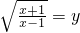 ,则原方程变为y-
,则原方程变为y- -
- =0,
=0,整理,得2y2-3y-2=0.
解得y1=-
 ,y2=2
,y2=2当y=-
 时,原方程无解.
时,原方程无解.当y=2时,
 =4,∴x=
=4,∴x=
经检验x=
 是原方程的根
是原方程的根∴原方程的根为x=

分析:原方程中的根式分别通分后,设
 =y,需要注意的是用来换元的式子为设
=y,需要注意的是用来换元的式子为设 ,则2y2-3y-2=0.
,则2y2-3y-2=0.点评:在解无理方程时最常用的方法是换元法,一般方法是通过观察确定用来换元的式子,例如本题中的
 =y.
=y. 
练习册系列答案
相关题目