题目内容
已知关于x的一元二次方程(m+2)x2-2(m-1)x+m=0有实数根,则m的取值范围是
- A.
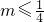
- B.
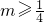
- C.

- D.

C
分析:由于一元二次方程有实数根,所以△≥0,再由此方程是一元二次方程可知m+2≠0,根据这两个条件求出m的取值范围即可.
解答:∵关于x的一元二次方程(m+2)x2-2(m-1)x+m=0有实数根,
∴△≥0,
即△=b2-4ac
=[-2(m-1)]2-4(m+2)m
=-16m+4≥0,
∴m≤ ,
,
∵此方程是一元二次方程,
∴m+2≠0,即m≠-2.
∴m的取值范围是: .
.
故选C.
点评:本题考查的是一元二次方程根的判别式,在解答此类题目时一定要注意二次项系数不为0,这是此题的易错点.
分析:由于一元二次方程有实数根,所以△≥0,再由此方程是一元二次方程可知m+2≠0,根据这两个条件求出m的取值范围即可.
解答:∵关于x的一元二次方程(m+2)x2-2(m-1)x+m=0有实数根,
∴△≥0,
即△=b2-4ac
=[-2(m-1)]2-4(m+2)m
=-16m+4≥0,
∴m≤
 ,
,∵此方程是一元二次方程,
∴m+2≠0,即m≠-2.
∴m的取值范围是:
 .
.故选C.
点评:本题考查的是一元二次方程根的判别式,在解答此类题目时一定要注意二次项系数不为0,这是此题的易错点.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
已知关于x的一元二次x2-6x+k+1=0的两个实数根x1,x2,
+
=1,则k的值是( )
| 1 |
| x1 |
| 1 |
| x2 |
| A、8 | B、-7 | C、6 | D、5 |
 .
. .
.