题目内容
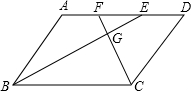
如图,四边形ABCD是平行四边形,BE平分∠ABC,CF平分∠BCD,BE、CF交于点G.若使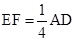 ,那么平行四边形ABCD应满足的条件是【 】
,那么平行四边形ABCD应满足的条件是【 】
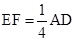 ,那么平行四边形ABCD应满足的条件是【 】
,那么平行四边形ABCD应满足的条件是【 】
| A.∠ABC=60° | B.AB:BC=1:4 | C.AB:BC=5:2 | D.AB:BC=5:8 |
D。
∵四边形ABCD是平行四边形,∴AD∥BC,AB=CD,AD=BC。∴∠AEB=∠EBC。
又BE平分∠ABC,∴∠ABE=∠EBC。∴∠ABE=∠AEB。∴AB=AE。
同理可得:DC=DF。
∴AE=DF。∴AE-EF=DE-EF,即AF=DE。
当 时,设EF=x,则AD=BC=4x。
时,设EF=x,则AD=BC=4x。
∴AF=DE= (AD-EF)=1.5x。∴AE=AB=AF+EF=2.5x。
(AD-EF)=1.5x。∴AE=AB=AF+EF=2.5x。
∴AB:BC=2.5:4=5:8。
∵以上各步可逆,∴当AB:BC=2.5:4=5:8时, 。故选D。
。故选D。
又BE平分∠ABC,∴∠ABE=∠EBC。∴∠ABE=∠AEB。∴AB=AE。
同理可得:DC=DF。
∴AE=DF。∴AE-EF=DE-EF,即AF=DE。
当
 时,设EF=x,则AD=BC=4x。
时,设EF=x,则AD=BC=4x。∴AF=DE=
 (AD-EF)=1.5x。∴AE=AB=AF+EF=2.5x。
(AD-EF)=1.5x。∴AE=AB=AF+EF=2.5x。∴AB:BC=2.5:4=5:8。
∵以上各步可逆,∴当AB:BC=2.5:4=5:8时,
 。故选D。
。故选D。
练习册系列答案
相关题目



 ,BC=26
,BC=26 的速度运动,动点Q从点C开始沿CB以3
的速度运动,动点Q从点C开始沿CB以3 ,问
,问 为何值时,(1)四边形PQCD是平行四边形.(2)当
为何值时,(1)四边形PQCD是平行四边形.(2)当
 中,
中, ,
, ,
,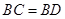 ,
, ,则
,则 ( )
( )



