题目内容
已知反比例函数y1=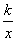 的图象与一次函数y2=ax+b的图象交于
的图象与一次函数y2=ax+b的图象交于
点A(1,4)和点B(m,﹣2),
(1)求这两个函数的关系式;
(2)观察图象,写出使得y1>y2成立的自变量x的取值范围;
(3)如果点C与点A关于x轴对称,求△ABC的面积.
解:(1)∵函数y1=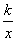 的图象过点A(1,4),即4=
的图象过点A(1,4),即4= ,
,
∴k=4,即y1= ,
,
又∵点B(m,﹣2)在y1= 上,∴m=﹣2,∴B(﹣2,﹣2),
上,∴m=﹣2,∴B(﹣2,﹣2),
又∵一次函数y2=ax+b过A、B两点,即  ,解之得
,解之得 .
.
∴y2=2x+2.
综上可得y1= ,y2=2x+2.
,y2=2x+2.
(2)要使y1>y2,即函数y1的图象总在函数y2的图象上方,
∴x<﹣2 或0<x<1.
(3) 由图形及题意可得:
由图形及题意可得:
AC=8,BD=3,
∴△ABC的面积S△ABC
= AC×BD=
AC×BD= ×8×3=12.
×8×3=12.

练习册系列答案
相关题目
计算(2a2)3的结果是( )
|
| A. | 2a6 | B. | 6a6 | C. | 8a6 | D. | 8a5 |
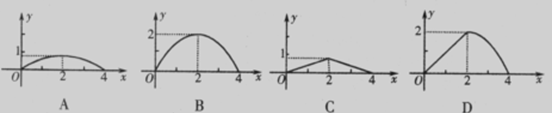


 .将他们组合成(A-B)÷C或 A-B÷C的形式,请你从中任选一种进行计算.先化简,再求值,其中x=3.
.将他们组合成(A-B)÷C或 A-B÷C的形式,请你从中任选一种进行计算.先化简,再求值,其中x=3.
 ,看到的标记是√的概率是多少
,看到的标记是√的概率是多少