题目内容
观察下列各式及其变形过程:
2
=
=
=
(1)按上述等式及其验证过程的基本思路,猜想3
的变形结果并进行证明;
(2)针对上述各式反映的规律,写出用n(n为自然数,n≥2)表示的算式,并证明;
(3)依上面规律,写出用n表示下列各式的规律:2
=
,3
=
,…(不要求证明).
2
|
|
|
2+
|
(1)按上述等式及其验证过程的基本思路,猜想3
|
(2)针对上述各式反映的规律,写出用n(n为自然数,n≥2)表示的算式,并证明;
(3)依上面规律,写出用n表示下列各式的规律:2
|
2-
|
|
3-
|
(1)从题目的变形可以得出3
=
=
=
.
证明:
=
=
=
=3
.所以变形正确.
(2)从上面两个变形可以看出3=22-1,8=32-1,
所以当为n时,分母为n2-1;
故当n≥2时,可以表示为n
=
;
证明:n
=
=
=
.
(3)有5=22+1,10=32+1;故当为n时有
n
=
|
|
|
3+
|
证明:
3+
|
|
|
|
|
(2)从上面两个变形可以看出3=22-1,8=32-1,
所以当为n时,分母为n2-1;
故当n≥2时,可以表示为n
|
n+
|
证明:n
|
|
|
n+
|
(3)有5=22+1,10=32+1;故当为n时有
n
|
n-
|

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
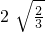 =
= =
=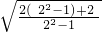 =
=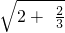
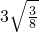 的变形结果并进行证明;
的变形结果并进行证明;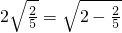 ,
,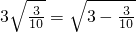 ,…(不要求证明).
,…(不要求证明).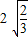 =
=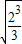 =
=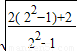 =
=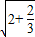
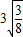 的变形结果并进行证明;
的变形结果并进行证明;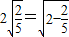 ,
,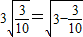 ,…(不要求证明).
,…(不要求证明).