题目内容
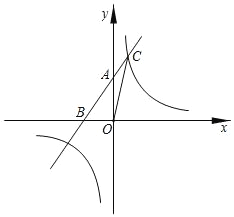
【题目】如图，直线y＝x+2与坐标轴相交于A，B两点，与反比例函数y＝
在第一象限交点C(1，a)．求：
（1）反比例函数的解析式；
（2）△AOC的面积；
（3）不等式x+2﹣＜0的解集（直接写出答案）
【答案】（1）y＝
;（2）1;（3）x＜﹣3或0＜x＜1.
【解析】
（1）将点C坐标分别代入直线y=x+2和反比例函数y=
，可求点C坐标，即可求反比例函数的解析式；
（2）由题意可得点A（0，2），点B（-2，0），即可求△AOC的面积；
（3）列出方程组可求直线y=x+2和反比例函数y=的交点坐标，根据图象可求不等式x+2-＜0的解集．
解：（1）∵点C（1，a）在直线y＝x+2上，
∴a＝1+2＝3
∴点C（1，3）
∵点C在反比例函数y＝图象上，
∴k＝1×3＝3
∴反比例函数的解析式y＝
（2）∵直线y＝x+2与坐标轴相交于A，B两点，
∴点A（0，2），点B（﹣2，0）
∴OA＝2
∴S△AOC＝
×1×2＝1
（3）∵
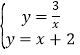
解得：
，
∴直线y＝x+2与反比例函数y＝的交点为（1，3），（﹣3，﹣1）
∴不等式x+2﹣＜0的解集为：x＜﹣3或0＜x＜1.
练习册系列答案
相关题目
【题目】物理兴趣小组
位同学在实验操作中的得分情况如下表：
得分(分) |
|
|
|
|
人数(人) |
|
|
|
|
问：（1）这位同学实验操作得分的众数是 ，中位数是
（2）这位同学实验操作得分的平均分是多少？
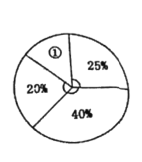
（3）将此次操作得分按人数制成如图所示的扇形统计图．扇形①的圆心角度数是多少？
