题目内容
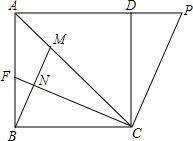 已知正方形ABCD如图所示,连接其对角线AC,∠BCA的平分线CF交AB于点F,过点B作BM⊥CF于点N,交AC于点M,过点C作CP⊥CF,交AD延长线于点P.
已知正方形ABCD如图所示,连接其对角线AC,∠BCA的平分线CF交AB于点F,过点B作BM⊥CF于点N,交AC于点M,过点C作CP⊥CF,交AD延长线于点P.
(1)若正方形ABCD的边长为4,求△ACP的面积;
(2)求证:CP=BM+2FN.
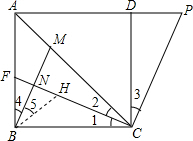 解:∵∠1=∠2=22.5°,又CP⊥CF,
解:∵∠1=∠2=22.5°,又CP⊥CF,∴∠3+∠FCD=∠1+∠FCD=90°
∴∠3=∠1=22.5°
∴∠P=67.5°
又四边形ABCD为正方形,
∴∠ACP=45+22.5=67.5°
∴∠P=∠ACP
∴AP=AC
又AC=
 AB=4
AB=4
∴AP=4
 ,
,∴S△APC=
 AP•CD=
AP•CD= 4
4 ×4=8
×4=8 ;
;(2)∵在△PDC和△FBC中,
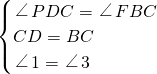
∴△PDC≌△FBC
∴CP=CF
在CN上截取NH=FN,连接BH
∵FN=NH,且BN⊥FH
∴BH=BF
∴∠4=∠5
∴∠4=∠1=∠5=22.5°
又∠4+∠BFC=∠1+∠BFC=90°
∴∠HBC=∠BAM=45°
在△AMB和△BHC中,
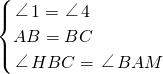 ,
,∴△AMB≌BHC,
∴CH=BM
∴CF=BM+2FN
∴CP=BM+2FN.
分析:(1)根据等角对等边易证AP=AC,根据勾股定理求得AC的长,然后根据三角形的面积公式即可求解;
(2)易证△PDC≌△FBC则CP=CF,在CN上截取NH=FN,连接BH,则可以证明△AMB≌BHC,得到CH=BM,即可证得.
点评:本题是正方形的性质,全等三角形的判定与性质以及勾股定理的综合应用,正确作出辅助线是关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
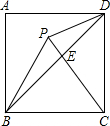 如图,已知正方形ABCD的边长为2,△BPC是等边三角形,则△CDP的面积是
如图,已知正方形ABCD的边长为2,△BPC是等边三角形,则△CDP的面积是
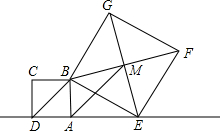 如图,已知正方形ABCD的边长为1,点E是射线DA一动点(DE>1),连结BE,以BE为边在BE上方作正方形BEFG,设M为正方形BEFG的中心,如果定义:只有一组对角是直角的四边形叫做损矩形.
如图,已知正方形ABCD的边长为1,点E是射线DA一动点(DE>1),连结BE,以BE为边在BE上方作正方形BEFG,设M为正方形BEFG的中心,如果定义:只有一组对角是直角的四边形叫做损矩形.