题目内容
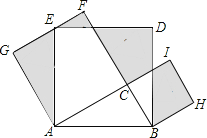
【题目】如图,![]() 中,
中,![]() 分别以
分别以![]() 为边在
为边在![]() 的同侧作正方形
的同侧作正方形![]() ,则图中阴影部分的面积之和为_______.
,则图中阴影部分的面积之和为_______.
【答案】![]()
【解析】
过D作BF的垂线交BF于N,连接DI,通过证明S1+S2+S3+S4=Rt△ABC的面积×3,依此即可求解.
解:过D作BF的垂线交BF于N,连接DI,
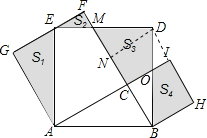
∵四边形![]() 、四边形
、四边形![]() 和四边形
和四边形![]() 为正方形,
为正方形,
∴GA=AC=GF,∠G=∠ABD=90°,AE=AB=BD,BC=CI,∠H=∠ICB=90°,
∵DN⊥BF,
∴∠DNB=90°,∠NDB+∠NBD=90°,
又∵∠ABD=∠NBA+∠NBD=90°,
∴∠NBA=∠NDB,
在△ACB和△BND中
∵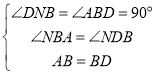
∴△ACB≌△BND(AAS),
∴BC=DN=IC,BN=AC,
又∵∠DNB=∠ICB=90°,
∴DN∥CI,
∴四边形DNCI是平行四边形,且平行四边形DNCI是矩形,
∴∠DIC=90°,
∴D、I、H三点共线,
∵∠ACB=90°,
∴∠G=∠ACB=90°,
在![]() 和
和![]() 中
中
∵![]()
∴![]() ≌
≌![]() (HL)
(HL)
∴GE=BC,
同理可证![]() ≌
≌![]() ,
,
∵∠BDE=∠ICB=90°,
∴∠DBM+∠DMB=90°,∠DBM+∠AOB=90°,
∴∠DMB=∠AOB,
∴∠EMF=∠DOI,
在△MND和△BCO中,
∵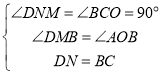
∴△MND≌△BCO,
∵DI=BN-BC,EF=GF-GE,
∴EF=DI,
在△EFM和△DIO中
∵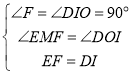
∴△EFM≌△DIO,
∵![]()
∴![]() ,
,
∴Rt△ABC的面积=![]() ,
,
∴S1+S2+S3+S4
=S1+S3+(S2+S4),
=Rt△ABC的面积+Rt△ABC的面积+Rt△ABC的面积
=Rt△ABC的面积×3=![]() ,
,
故答案为:![]() .
.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案【题目】“2018东台西溪半程马拉松”的赛事共有两项:A、“半程马拉松”、 B、“欢乐跑”。小明参加了该项赛事的志愿者服务工作, 组委会随机将志愿者分配到两个项目组.
(1)小明被分配到“半程马拉松”项目组的概率为________.
(2)为估算本次赛事参加“半程马拉松”的人数,小明对部分参赛选手作如下调查:
调查总人数 | 20 | 50 | 100 | 200 | 500 |
参加“半程马拉松”人数 | 15 | 33 | 72 | 139 | 356 |
参加“半程马拉松”频率 | 0.750 | 0.660 | 0.720 | 0.695 | 0.712 |
①请估算本次赛事参加“半程马拉松”人数的概率为_______.(精确到0.1)
②若本次参赛选手大约有3000人,请你估计参加“半程马拉松”的人数是多少?