Question

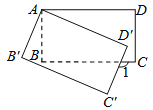
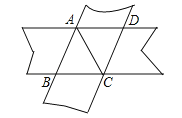
【题目】某校门前正对一条公路，车流量较大，为便于学生安全通过，特建一座人行天桥．如图，是这座天桥的引桥部分示意图，上桥通道由两段互相平行的楼梯AB、CD和一段平行于地面的平台CB构成．已知∠A=37°，天桥高度DH为5.1米，引桥水平跨度AH为8.3米．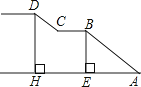

（1）求水平平台BC的长度；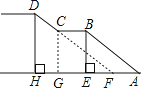

（2）若两段楼梯AB：CD=10：7，求楼梯AB的水平宽度AE的长．
（参考数据：sin37°≈ ，cos37°≈ ，tan37°≈ ）

Answer 1

【答案】
（1）

解：延长DC交AH于F，

根据题意得，四边形BCFA为平行四边形，

故BC=AF，BA=CF，

∵BA∥CF，

∴∠HFC=∠A=37°，

在RT△DHF中，DH=5.1，

∴HF= ═6.8（m），

∴BC=AH﹣HF=1.5（m）

（2）

解：如图

作CG⊥AH于G，得CG=BE，

∵CG∥DH，

∴△FCG∽△FDH，

∴ ，

∵AB：CD=10：7，

∴ ，

∴CG=3，

∴AE= =4米

【解析】（1）延长DC交AH于F，根据题意得，四边形BCFA为平行四边形，在RT△DHF中，求出HF，则可得出BC的长度．（2）先判断出△FCG∽△FDH，然后根据AB：CD=10：7，可得出 = ，继而可解出CG的长度，也可得出AE的长．
【考点精析】掌握关于坡度坡角问题是解答本题的根本，需要知道坡面的铅直高度h和水平宽度l的比叫做坡度(坡比)．用字母i表示，即i=h/l．把坡面与水平面的夹角记作A(叫做坡角)，那么i=h/l=tanA．